
The area enclosed by the curve \[{{y}^{2}}+{{x}^{4}}={{x}^{2}}\] is:
\[\begin{align}
& (\text{A})\text{ }\dfrac{2}{3} \\
& (B)\text{ }\dfrac{4}{3} \\
& (C)\text{ }\dfrac{8}{3} \\
& (D)\text{ }\dfrac{10}{3} \\
\end{align}\]
Answer
573.6k+ views
Hint: First, try to make a rough sketch. Then find out the symmetry. Then find the area under the curve using the formula; Finding the area enclosed by $f(x)$ between $x=a$ and $x=b$ can be written as $=|\int\limits_{a}^{b}{f(x)dx|}$.
Complete step by step answer:
Consider the given curve,
\[{{y}^{2}}+{{x}^{4}}={{x}^{2}}\]
Put \[y=-y\]and note that the expression remains unchanged. So the curve is symmetric about the x-axis.
Similarly, the curve is symmetric about the y-axis.
So, we can write the curve as,
\[\begin{align}
& {{y}^{2}}+{{x}^{4}}={{x}^{2}} \\
& \Rightarrow {{y}^{2}}={{x}^{2}}-{{x}^{4}} \\
& \Rightarrow {{y}^{2}}={{x}^{2}}(1-{{x}^{2}}) \\
\end{align}\]
Squaring on both sides, we get
\[y=x\sqrt{1-{{x}^{2}}}\]
So, first of all let’s try plotting the curve considering various values,
Note that at\[x=0,y=0\]
And at \[y=0,\left( 1-x \right)\left( 1+x \right)=0\]or \[x=1,-1\]
We will consider one more point,
\[\begin{align}
& x=0.5 \\
& \Rightarrow y=\sqrt{{{\left( 0.5 \right)}^{2}}\left( 1-{{(0.5)}^{2}} \right)} \\
& \Rightarrow y=\pm 0.43 \\
\end{align}\]
Similarly,
\[\begin{align}
& x=-0.5 \\
& \Rightarrow y=\sqrt{{{\left( -0.5 \right)}^{2}}\left( 1-{{(-0.5)}^{2}} \right)} \\
& \Rightarrow y=\pm 0.43 \\
\end{align}\]
So, the points calculated are,

Use the above observations to plot the graph.
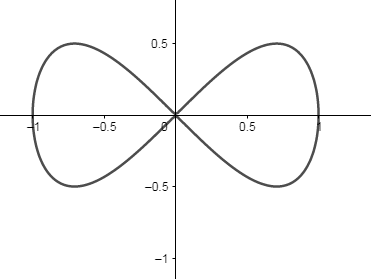
We can see that the area is symmetrical about x-axis and y-axis. So the curve can be divided into four parts. So we can now find the area by integrating the function from $x=0$to $x=1$. Then multiply it by four to get the total area under the curve.
The formula of finding the area enclosed by $f(x)$ between $x=a$ and $x=b$ can be written as $=|\int\limits_{a}^{b}{f(x)dx|}$.
So the required area under the curve is,
\[\text{Area}=\int\limits_{0}^{1}{x\sqrt{1-{{x}^{2}}}dx}.........(i)\]
Put \[1-{{x}^{2}}={{u}^{2}}\]
Differentiating on both sides, we get
\[\Rightarrow -2x\text{ }dx=2u\text{ }du\]
\[\Rightarrow x\text{ }dx=-u\text{ }du\]
Now we will find the limits, when this value is substituted.
When
$\begin{align}
& x=0 \\
& \Rightarrow (1-{{0}^{2}})={{u}^{2}} \\
& \Rightarrow u=1 \\
\end{align}$
When
$\begin{align}
& x=1 \\
& \Rightarrow (1-{{1}^{2}})={{u}^{2}} \\
& \Rightarrow u=0 \\
\end{align}$
Substituting these values in equation (i), we get
\[\text{Area}=\int\limits_{1}^{0}{\sqrt{{{u}^{2}}}\left( -udu \right)}\]
\[\text{Area }=-\int\limits_{1}^{0}{{{u}^{2}}\text{ }du}\]
On integrating, we get
\[Area=-\left[ \dfrac{{{u}^{3}}}{3} \right]_{1}^{0}\]
Applying the limits, we get
\[Area=-\left[ \dfrac{{{0}^{3}}}{3}-\dfrac{{{1}^{3}}}{3} \right]\]
\[Area=\dfrac{1}{3}\text{ sq}\text{. units}\]
Note that the above area is for the first quadrant. As we need the entire area enclosed by the curve, so multiply the area by \[4\], we get
\[\text{Total Area}=4\times \dfrac{1}{3}\text{=}\dfrac{4}{3}\text{ sq}\text{. units}\]
So, the correct answer is “$\dfrac{4}{3}$”.
Note: The possibility of mistake is that the student might not multiply the result by \[4\]. One more possibility is the students forget to change the limits when substituting with ‘u’.
Instead of the is\[\text{Area }=-\int\limits_{1}^{0}{{{u}^{2}}\text{ }du}\], they will write \[\text{Area }=-\int\limits_{0}^{1}{{{u}^{2}}\text{ }du}\]. They will get a negative answer.
Complete step by step answer:
Consider the given curve,
\[{{y}^{2}}+{{x}^{4}}={{x}^{2}}\]
Put \[y=-y\]and note that the expression remains unchanged. So the curve is symmetric about the x-axis.
Similarly, the curve is symmetric about the y-axis.
So, we can write the curve as,
\[\begin{align}
& {{y}^{2}}+{{x}^{4}}={{x}^{2}} \\
& \Rightarrow {{y}^{2}}={{x}^{2}}-{{x}^{4}} \\
& \Rightarrow {{y}^{2}}={{x}^{2}}(1-{{x}^{2}}) \\
\end{align}\]
Squaring on both sides, we get
\[y=x\sqrt{1-{{x}^{2}}}\]
So, first of all let’s try plotting the curve considering various values,
Note that at\[x=0,y=0\]
And at \[y=0,\left( 1-x \right)\left( 1+x \right)=0\]or \[x=1,-1\]
We will consider one more point,
\[\begin{align}
& x=0.5 \\
& \Rightarrow y=\sqrt{{{\left( 0.5 \right)}^{2}}\left( 1-{{(0.5)}^{2}} \right)} \\
& \Rightarrow y=\pm 0.43 \\
\end{align}\]
Similarly,
\[\begin{align}
& x=-0.5 \\
& \Rightarrow y=\sqrt{{{\left( -0.5 \right)}^{2}}\left( 1-{{(-0.5)}^{2}} \right)} \\
& \Rightarrow y=\pm 0.43 \\
\end{align}\]
So, the points calculated are,

Use the above observations to plot the graph.
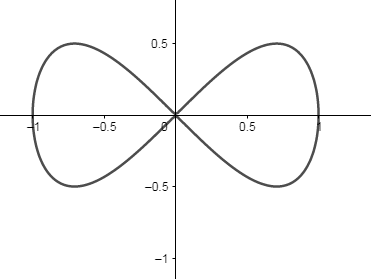
We can see that the area is symmetrical about x-axis and y-axis. So the curve can be divided into four parts. So we can now find the area by integrating the function from $x=0$to $x=1$. Then multiply it by four to get the total area under the curve.
The formula of finding the area enclosed by $f(x)$ between $x=a$ and $x=b$ can be written as $=|\int\limits_{a}^{b}{f(x)dx|}$.
So the required area under the curve is,
\[\text{Area}=\int\limits_{0}^{1}{x\sqrt{1-{{x}^{2}}}dx}.........(i)\]
Put \[1-{{x}^{2}}={{u}^{2}}\]
Differentiating on both sides, we get
\[\Rightarrow -2x\text{ }dx=2u\text{ }du\]
\[\Rightarrow x\text{ }dx=-u\text{ }du\]
Now we will find the limits, when this value is substituted.
When
$\begin{align}
& x=0 \\
& \Rightarrow (1-{{0}^{2}})={{u}^{2}} \\
& \Rightarrow u=1 \\
\end{align}$
When
$\begin{align}
& x=1 \\
& \Rightarrow (1-{{1}^{2}})={{u}^{2}} \\
& \Rightarrow u=0 \\
\end{align}$
Substituting these values in equation (i), we get
\[\text{Area}=\int\limits_{1}^{0}{\sqrt{{{u}^{2}}}\left( -udu \right)}\]
\[\text{Area }=-\int\limits_{1}^{0}{{{u}^{2}}\text{ }du}\]
On integrating, we get
\[Area=-\left[ \dfrac{{{u}^{3}}}{3} \right]_{1}^{0}\]
Applying the limits, we get
\[Area=-\left[ \dfrac{{{0}^{3}}}{3}-\dfrac{{{1}^{3}}}{3} \right]\]
\[Area=\dfrac{1}{3}\text{ sq}\text{. units}\]
Note that the above area is for the first quadrant. As we need the entire area enclosed by the curve, so multiply the area by \[4\], we get
\[\text{Total Area}=4\times \dfrac{1}{3}\text{=}\dfrac{4}{3}\text{ sq}\text{. units}\]
So, the correct answer is “$\dfrac{4}{3}$”.
Note: The possibility of mistake is that the student might not multiply the result by \[4\]. One more possibility is the students forget to change the limits when substituting with ‘u’.
Instead of the is\[\text{Area }=-\int\limits_{1}^{0}{{{u}^{2}}\text{ }du}\], they will write \[\text{Area }=-\int\limits_{0}^{1}{{{u}^{2}}\text{ }du}\]. They will get a negative answer.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Differentiate between action potential and resting class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




