Question

The area between the parabola \[y = {x^2}\]and the line \[y = x\]is
(a) $\dfrac{1}{6}$sq. unit
(b) $\dfrac{1}{3}$sq. unit
(c) $\dfrac{1}{2}$sq. unit
(d) None of these

Answer 1

Hint: Equate the parabola and line equations to find the coordinates. Using these coordinates draw a line which passes through a parabola to find the area.

The given equations are
\[y = {x^2}\] …(1)
\[y = x\] …(2)
To find the point where the line cuts the parabola, let us substitute equation (2) in (1) and find the coordinates.

We get,
\[\begin{gathered}
  x = {x^2} \\
  {x^2} - x = 0 \\
  x(x - 1) = 0 \\
  x = 0,x = 1 \\
\end{gathered} \]
Now for \[{\text{x}} = 0\]and\[{\text{x}} = {\text{1}}\], we need to find the y coordinate values. From equation (2), \[y = x\].
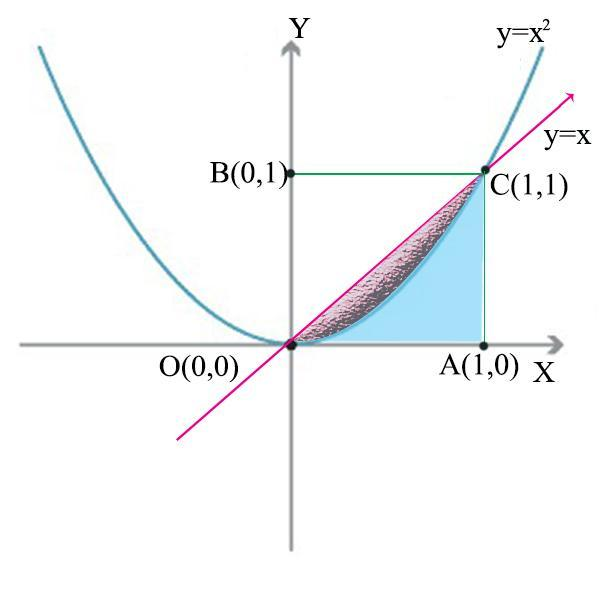
Hence, the coordinates are (0,0) and (1,1) and let the points be denoted as O(0,0) and C(1,1).
Drop perpendiculars from C to X-axis to meet it at A (1,0) and to Y-axis to meet it at B (0,1) as shown in the figure.
Required area=Pink shaded region between the parabola and the line.
We will find the area of the right-angled triangle OAC and subtract the blue shaded area using integration in order to get the required area (pink region).
Area of the right-angled triangle OAC (Pink area+Blue area) =$\dfrac{1}{2} \times OA \times AC$
=$\dfrac{1}{2} \times 1 \times 1$
=$\dfrac{1}{2}$sq. unit …(3)
Area under the parabola and within the lines OA and OC (Blue area) \[ = \mathop \smallint \limits_0^1 y.dx\]
\[ = \mathop \smallint \limits_0^1 {x^2}.dx\]
\[\begin{gathered}
   = [\dfrac{{{x^3}}}{3}]_0^1 \\
   = \dfrac{1}{3} - 0 \\
\end{gathered} \]
\[ = \dfrac{1}{3}\]sq. unit …(4)
To get the required area, subtract equation (4) from (3)
Required area (Pink area)$\begin{gathered}
   = \dfrac{1}{2} - \dfrac{1}{3} \\
    \\
\end{gathered} $
$ = \dfrac{1}{6}$sq. unit
Option (1) is the correct answer.
Note: Common mistake that students tend to make in this problem is identifying the correct area which is asked for. They tend to misunderstand that the required area is the entire area under the line\[y = x\]and between the X-axis.