Question

The angle of elevation of the top of the tower from the point $a$ meter away from the base of the tower is ${{60}^{\circ }}$. The height of the tower is __________ meter.
(a) $\dfrac{1}{\sqrt{3}}a$
(b) $2a$
(c) $\sqrt{3}a$
(d) $a$

Answer 1

Hint: First we have to draw a rough diagram of the given situation. The diagram will look like a right angled triangle with one of the sides $=a$. Let us assume the height of the tower is ‘$h$’. Then use $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$ to calculate the height of the tower in the right angled triangle.


Complete step-by-step answer:
First we have to understand the meaning of angle of elevation. The angle of elevation is the angle made by the line of sight with the horizontal when we are looking above the horizon. We have to use basic concepts of trigonometry and triangles. Also remembering values of trigonometric functions at some particular angles will help in this type of problem.

We assume that the tower \[\text{AB}\]is of height ‘$h$’.

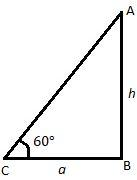
Assuming that the man is looking at the top of the tower, which is point \[\text{A}\] and his eyes are making an angle of ${{60}^{\circ }}$ with the horizontal or ground level. Therefore triangle \[\text{ABC}\] forms a right angled triangle with $\angle C={{60}^{\circ }}$.
Now, we have been given $\text{BC}=a\text{ meters}$ and we have to find \[\text{AB}=h\].
Now in a triangle, $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$.
$\begin{align}
  & \because \theta ={{60}^{\circ }} \\
 & \therefore \tan {{60}^{\circ }}=\dfrac{h}{a} \\
 & \therefore \sqrt{3}=\dfrac{h}{a} \\
 & \therefore h=\sqrt{3}a \\
\end{align}$
Hence, the correct option is option (c).

Note: One should properly remember the values of trigonometric functions at some particular angles like values of $\sin \theta ,\text{ }\cos \theta \text {and }\tan \theta $ at angles $0{}^\circ ,30{}^\circ ,45{}^\circ ,60{}^\circ \text { and }90{}^\circ $. Heights and distance problems are mainly based on these concepts.