Question

The angle of elevation of an electric pole from a point A to the ground is 60° and from a point B towards the pole on the line joining the foot of the pole to the point is 75°. If the distance AB = a, then the height of the pole is :
A.$\dfrac{{a\left( {3 + 2\sqrt 3 } \right)}}{2}$
B.$a\left( {4 + 2\sqrt 3 } \right)$
C.$\dfrac{{a\left( {2 + \sqrt 3 } \right)}}{2}$
D.$\dfrac{{a\left( {2\sqrt 3 - 3} \right)}}{2}$

Answer 1

Hint: We will first draw the figure of the given condition and then we will use the formula of $\tan \theta = \dfrac{{perpendicular}}{{base}}$ in both the given angles of tan using the formula of tan(a+b) = $\dfrac{{\tan a + \tan b}}{{1 - \tan a\tan b}}$ and then from the obtained two equations, we will determine the value of height.

Complete step-by-step answer:
We are given the angle of elevation of an electric pole from a point A from the ground is given as 60° .
Also, the angle of elevation made by point B from the line joining the foot of the pole is 75°.
We are given the distance between the points A and B is AB = a.
Let us draw the figure:

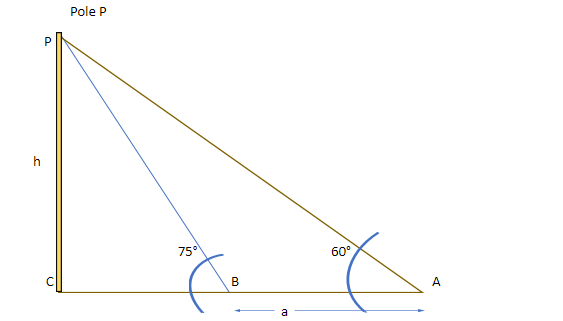
let us assume that distance BC = x
hence, in triangle BCP, $\tan 75^\circ = \dfrac{h}{b}$
Now, tan 75° can be written as $\tan (45^\circ + 30^\circ )$
We can further solve it as $\tan (45^\circ + 30^\circ ) = \dfrac{{\tan 45^\circ + \tan 30^\circ }}{{1 - \tan 45^\circ \tan 30^\circ }}$ using the formula tan (a + b) = $\dfrac{{\tan a + \tan b}}{{1 - \tan a\tan b}}$.
$
   \Rightarrow \tan ({45^ \circ } + {30^ \circ }) = \dfrac{{1 + \dfrac{1}{{\sqrt 3 }}}}{{1 - 1(\dfrac{1}{{\sqrt 3 }})}} \\
   \Rightarrow \tan {75^ \circ } = \dfrac{{\sqrt 3 + 1}}{{\sqrt 3 - 1}} = \dfrac{{\left( {\sqrt 3 + 1} \right)\left( {\sqrt 3 + 1} \right)}}{{3 - 1}} = \dfrac{{3 + 1 + 2\sqrt 3 }}{2} = \dfrac{{2\left( {2 + \sqrt 3 } \right)}}{2} = \left( {2 + \sqrt 3 } \right) \\
 $
Therefore, tan75$^ \circ $= $\dfrac{h}{b} = \left( {2 + \sqrt 3 } \right)$
$ \Rightarrow b = \dfrac{h}{{2 + \sqrt 3 }}$
Now, in triangle ACP, tan 60$^ \circ $= $\dfrac{h}{{a + b}}$
Substituting the values of b and tan 60$^ \circ $, we get
$
   \Rightarrow \sqrt 3 = \dfrac{h}{{a + b}} \\
   \Rightarrow h = \sqrt 3 \left( {a + b} \right) \\
   \Rightarrow h = \sqrt 3 \left( {a + \dfrac{h}{{2 + \sqrt 3 }}} \right) \\
   \Rightarrow h - \dfrac{{h\sqrt 3 }}{{2 + \sqrt 3 }} = a\sqrt 3 \\
   \Rightarrow h\left( {\dfrac{{2 + \sqrt 3 - \sqrt 3 }}{{2 + \sqrt 3 }}} \right) = a\sqrt 3 \\
 $
Simplifying it further for the value of h, we get
$\therefore h = \dfrac{{a\left( {3 + 2\sqrt 3 } \right)}}{2}$
Therefore, the height of the pole h is found to be $\dfrac{{a\left( {3 + 2\sqrt 3 } \right)}}{2}$

Note: You should not get confused while calculating the tan75$^ \circ $with tan45$^ \circ $+ tan30$^ \circ $ instead of tan(45$^ \circ $+ tan30$^ \circ $). Be careful while simplifying for h because there are further calculations based on h value. If h value is wrong the final answer will come wrong.