Question

The acceleration of a moving body can be found from:
(A) Slope of velocity-time graph
(B) Area under velocity-time graph
(C) Slope of distance-time graph
(D) Area under distance-time graph

Answer 1

Hint: We will use the basic definition of acceleration in order to solve this question which states that the rate of change in velocity of an object gives the acceleration. This is a vector quantity which is having both magnitude and direction. This will help you in solving this question.

Complete step-by-step solution
The acceleration can be figured out by taking the rate of variation of the velocity of a body with respect to the time taken. When a body is moving from one point to another at a specific time, its velocity will change. Because a body is going from one point to another and the change in velocity does not keep on constant. Therefore the slope of the velocity-time curve will be equivalent to the tangent of the angle between the curve and time axis. This will be comparable to the first derivative of the velocity.
 $ \tan \theta = \dfrac{{dv}}{{dt}} $
where $ \theta $ be the angle between the curve and the time axis. For that reason, the slope of a velocity-time graph will be the acceleration. This has been mentioned as an option (A).

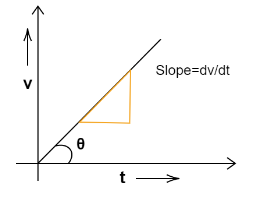
So, the correct answer is option (A) Slope of the velocity-time graph.

Note
The slope of the line on a velocity-time graph depicts valuable information about the acceleration of the body. When the acceleration is zero, then the slope also tends to be zero. That means the horizontal line. If the acceleration is positive, the slope will also be positive. Also, recall that the area under the velocity-time graph provides the distance covered by the object.