Question

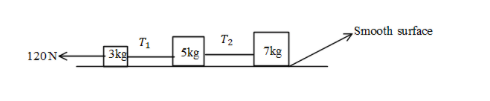
${T_1}$ and ${T_2}$ in the given figure are:

A) 28N, 48N.
B) 48N, 28N.
C) 96N, 56N.
D) 56N, 96N.

Answer 1

Hint:The smooth surface does not provide friction on the surface between the bodies of the blocks. If the surface has friction force between the blocks then the equations that we are going to make will have an extra term and that will be friction force.

Formula used:The formula of the force is given by,
$ \Rightarrow F = m \times a$
Where force is F, the mass is m and the acceleration is a.

Step by step solution:
It is given in the problem that there are three blocks and there are two ropes which are tied by a rope and we need to find the tension in the rope.
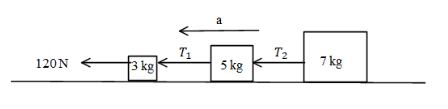
Let us see the free body diagram of the above problem.

The formula of the force is given by,

$ \Rightarrow F = m \times a$

Where force is F, the mass is m and the acceleration is a.
As all the blocks will move with each other therefore total mass is,

$ \Rightarrow m = 3 + 5 + 7$
$ \Rightarrow m = 15kg$

And the applied force is 120N.

$ \Rightarrow F = m \times a$
$ \Rightarrow 120 = 15 \times a$
$ \Rightarrow a = \dfrac{{120}}{{15}}\dfrac{m}{{{s^2}}}$.
$ \Rightarrow a = 8\dfrac{m}{{{s^2}}}$.

Free body diagram of block of mass 3 kg.

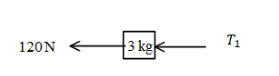
$ \Rightarrow 120 - {T_1} = {m_1} \times a$.

The mass is 3 kg and the acceleration is $a = 8\dfrac{m}{{{s^2}}}$.

$ \Rightarrow 120 - {T_1} = {m_1} \times a$
$ \Rightarrow 120 - {T_1} = 3 \times 8$
$ \Rightarrow 120 - {T_1} = 24$
$ \Rightarrow {T_1} = 96N$.

Free body diagram of the body of mass 5 kg.

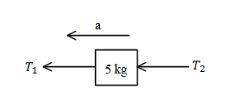
$ \Rightarrow {T_1} - {T_2} = {m_2} \times a$

Mass of the block is 5 kg and acceleration is $a = 8\dfrac{m}{{{s^2}}}$.

$ \Rightarrow {T_1} - {T_2} = {m_2} \times a$
$ \Rightarrow 96 - {T_2} = 5 \times 8$
$ \Rightarrow 96 - {T_2} = 40$
$ \Rightarrow {T_2} = 56N$.

The tension of the strings are ${T_1} = 96N$ and ${T_2} = 56N$.

The correct answer for this problem is option C.

Note:The tension always acts always from the body. All the bodies will move with each other and therefore all the bodies will have the same acceleration. The equations that are based on the motion of the blocks should be designed very carefully.