Statement-1: If the middle point of the sides of a triangle ABC are ( 0,0), ( 1,2), ( -3,4) then centroid of $\Delta ABC$ is $\left( \dfrac{-2}{3},2 \right)$.
Statement-2: Centroid of a triangle ABC and centroid of the triangle formed by joining the mid points of sides of triangle ABC be always the same .
A) Statement $-1$ is True. Statement $-2$ True: Statement $-2$ is a correct explanation for statement$-1$.
B) Statement $-1$ is True. Statement $-2$ True: Statement $-2$ is not correct explanation for statement $-1$
C) Statement $-1$ is True. Statement $-2$ False
D) Statement $-1$ is False. Statement $-2$ True
Answer
Verified606.6k+ views
Hint: The coordinates of centroid of a triangle with vertices $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)$ is given as $\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$ .
Statement-1: The given triangle is $\Delta ABC$. We will consider the vertices of $\Delta ABC$ to be given as $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)\ and C\left( {{x}_{3}},{{y}_{3}} \right)$.
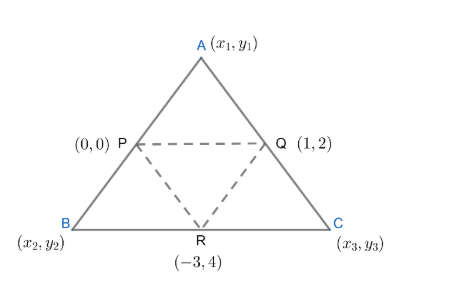
Now , from the diagram , we can see that $P,Q,R$ are the midpoints of sides $AB,AC$ and $BC$ respectively .
Now , we know that the midpoint of line joining $\left( {{a}_{1}},{{b}_{1}} \right)\ and \left( {{a}_{2}},{{b}_{2}} \right)$ is given as
$\left( \dfrac{{{a}_{1}}+{{a}_{2}}}{2},\dfrac{{{b}_{1}}+{{b}_{2}}}{2} \right)$
So , midpoint of $AB$ i.e., $P$ is given as
\[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]
But , in the question , it is given that coordinates of $P$ are $\left( 0,0 \right)$.
So , $\dfrac{{{x}_{1}}+{{x}_{2}}}{2}=0\Rightarrow {{x}_{1}}+{{x}_{2}}=0.........\left( i \right)$
And $\dfrac{{{y}_{1}}+{{y}_{2}}}{2}=0\Rightarrow {{y}_{1}}+{{y}_{2}}=0.........\left( ii \right)$
Again , midpoint of $AC$ is $Q$. So , the coordinates of $Q$ are given as
\[\left( \dfrac{{{x}_{1}}+{{x}_{3}}}{2},\dfrac{{{y}_{1}}+{{y}_{3}}}{2} \right)\]
But in the question, coordinates of $Q$ are given as $\left( 1,2 \right)$.
So , $\begin{align}
& \dfrac{{{x}_{1}}+{{x}_{3}}}{2}=1\Rightarrow {{x}_{1}}+{{x}_{3}}=2......\left( iii \right) \\
& \\
\end{align}$
And $\dfrac{{{y}_{1}}+{{y}_{2}}}{2}=2\Rightarrow {{y}_{1}}+{{y}_{3}}=4........\left( iv \right)$
Again , midpoint of $BC$ is $R$. So , the coordinates of $R$ are given as
\[\left( \dfrac{{{x}_{2}}+{{x}_{3}}}{2},\dfrac{{{y}_{2}}+{{y}_{3}}}{2} \right)\]
But in the question, coordinates of $R$ are given as $\left( -3,4 \right)$.
So, $\dfrac{{{x}_{2}}+{{x}_{3}}}{2}=-3\Rightarrow {{x}_{2}}+{{x}_{3}}=-6..........\left( v \right)$
And $\dfrac{{{y}_{2}}+{{y}_{3}}}{2}=4\Rightarrow {{y}_{2}}+{{y}_{3}}=8..........\left( vi \right)$
Now , we will add the equations $\left( i \right),\left( iii \right)$ and $\left( v \right)$.
On adding equations $\left( i \right),\left( iii \right)$ and $\left( v \right)$ , we get
$\begin{align}
& {{x}_{1}}+{{x}_{2}}+{{x}_{1}}+{{x}_{3}}+{{x}_{2}}+{{x}_{3}}=0+2+\left( -6 \right) \\
& \Rightarrow 2\left( {{x}_{1}}+{{x}_{2}}+{{x}_{3}} \right)=-4 \\
& \Rightarrow \left( {{x}_{1}}+{{x}_{2}}+{{x}_{3}} \right)=-2...........\left( vii \right) \\
\end{align}$
Now , we will add the equations $\left( ii \right),\left( iv \right)$and $\left( vi \right)$.
On adding equations $\left( ii \right),\left( iv \right)$and $\left( vi \right)$, we get
$\begin{align}
& {{y}_{1}}+{{y}_{2}}+{{y}_{1}}+{{y}_{3}}+{{y}_{2}}+{{y}_{3}}=0+4+8 \\
& \Rightarrow 2\left( {{y}_{1}}+{{y}_{2}}+{{y}_{3}} \right)=12 \\
& \Rightarrow \left( {{y}_{1}}+{{y}_{2}}+{{y}_{3}} \right)=6...................\left( viii \right) \\
\end{align}$
Now , we know the coordinates of centroid of a triangle with vertices $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)$ is given as $\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$ .
So , the coordinates of centroid of $\Delta ABC$is
$G\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$
But , from equations $\left( vii \right)$and $\left( viii \right)$, we have
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}=-2$ and ${{\text{y}}_{1}}+{{y}_{2}}+{{y}_{3}}=6\text{ }$
So , coordinates of the centroid of $\Delta ABC$are $G\left( \dfrac{-2}{3},2 \right)$ .
Hence , the statement $\left( 1 \right)$ is true.
Statement $2$: Let the vertices of triangle be $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)\And C\left( {{x}_{3}},{{y}_{3}} \right)$
So the midpoint of $AB$ is $D\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ , $\text{BC}$ is $\text{E}\left( \dfrac{{{x}_{2}}+{{x}_{3}}}{2},\dfrac{{{y}_{2}}+{{y}_{3}}}{2} \right)$ and $AC$ is $\text{F}\left( \dfrac{{{x}_{1}}+{{x}_{3}}}{2},\dfrac{{{y}_{1}}+{{y}_{3}}}{2} \right)$.
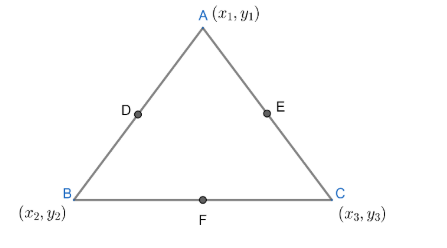
Now , we will find the centroid of $\Delta ABC$.
We know the coordinates of centroid of a triangle with vertices $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)$ is given as $\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$.
So , the centroid of $\Delta ABC$ is \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\] .
Now , we will find the centroid of $\Delta DEF$.
The centroid of $\Delta DEF$ is given as $\left( \dfrac{\dfrac{{{x}_{1}}+{{x}_{2}}}{2}+\dfrac{{{x}_{2}}+{{x}_{3}}}{2}+\dfrac{{{x}_{3}}+{{x}_{1}}}{2}}{3},\dfrac{\dfrac{{{y}_{1}}+{{y}_{2}}}{2}+\dfrac{{{y}_{3}}+{{y}_{2}}}{2}+\dfrac{{{y}_{1}}+{{y}_{3}}}{2}}{3} \right)$
$=\left( \dfrac{\dfrac{2\left( {{x}_{1}}+{{x}_{2}}+{{x}_{3}} \right)}{2}}{3},\dfrac{\dfrac{2\left( {{y}_{1}}+{{y}_{2}}+{{y}_{3}} \right)}{2}}{3} \right)$
$=\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$
= centroid of $\Delta ABC$.
Hence , the statement $\left( 2 \right)$ is true.
So , we can conclude that statement $\left( 1 \right)$ is true, statement $\left( 2 \right)$ is true and statement $\left( 2 \right)$ is a correct explanation for statement$\left( 1 \right)$.
So, (1) Statement $\left( 1 \right)$ is true, statement $\left( 2 \right)$ is true; statement $\left( 2 \right)$ is a correct explanation for statement $\left( 1 \right)$.
Note: The midpoint of line joining the points $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ is given as:
$\left( \dfrac{\left( {{x}_{1}}+{{x}_{2}} \right)}{2},\dfrac{\left( {{y}_{1}}+{{y}_{2}} \right)}{2} \right)$ and not $\left( \dfrac{\left( {{x}_{1}}-{{x}_{2}} \right)}{2},\dfrac{\left( {{y}_{1}}-{{y}_{2}} \right)}{2} \right)$ . Students often get confused between the two. Due to this confusion , they generally end up getting a wrong answer . So , such mistakes should be avoided .
Statement-1: The given triangle is $\Delta ABC$. We will consider the vertices of $\Delta ABC$ to be given as $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)\ and C\left( {{x}_{3}},{{y}_{3}} \right)$.
Now , from the diagram , we can see that $P,Q,R$ are the midpoints of sides $AB,AC$ and $BC$ respectively .
Now , we know that the midpoint of line joining $\left( {{a}_{1}},{{b}_{1}} \right)\ and \left( {{a}_{2}},{{b}_{2}} \right)$ is given as
$\left( \dfrac{{{a}_{1}}+{{a}_{2}}}{2},\dfrac{{{b}_{1}}+{{b}_{2}}}{2} \right)$
So , midpoint of $AB$ i.e., $P$ is given as
\[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]
But , in the question , it is given that coordinates of $P$ are $\left( 0,0 \right)$.
So , $\dfrac{{{x}_{1}}+{{x}_{2}}}{2}=0\Rightarrow {{x}_{1}}+{{x}_{2}}=0.........\left( i \right)$
And $\dfrac{{{y}_{1}}+{{y}_{2}}}{2}=0\Rightarrow {{y}_{1}}+{{y}_{2}}=0.........\left( ii \right)$
Again , midpoint of $AC$ is $Q$. So , the coordinates of $Q$ are given as
\[\left( \dfrac{{{x}_{1}}+{{x}_{3}}}{2},\dfrac{{{y}_{1}}+{{y}_{3}}}{2} \right)\]
But in the question, coordinates of $Q$ are given as $\left( 1,2 \right)$.
So , $\begin{align}
& \dfrac{{{x}_{1}}+{{x}_{3}}}{2}=1\Rightarrow {{x}_{1}}+{{x}_{3}}=2......\left( iii \right) \\
& \\
\end{align}$
And $\dfrac{{{y}_{1}}+{{y}_{2}}}{2}=2\Rightarrow {{y}_{1}}+{{y}_{3}}=4........\left( iv \right)$
Again , midpoint of $BC$ is $R$. So , the coordinates of $R$ are given as
\[\left( \dfrac{{{x}_{2}}+{{x}_{3}}}{2},\dfrac{{{y}_{2}}+{{y}_{3}}}{2} \right)\]
But in the question, coordinates of $R$ are given as $\left( -3,4 \right)$.
So, $\dfrac{{{x}_{2}}+{{x}_{3}}}{2}=-3\Rightarrow {{x}_{2}}+{{x}_{3}}=-6..........\left( v \right)$
And $\dfrac{{{y}_{2}}+{{y}_{3}}}{2}=4\Rightarrow {{y}_{2}}+{{y}_{3}}=8..........\left( vi \right)$
Now , we will add the equations $\left( i \right),\left( iii \right)$ and $\left( v \right)$.
On adding equations $\left( i \right),\left( iii \right)$ and $\left( v \right)$ , we get
$\begin{align}
& {{x}_{1}}+{{x}_{2}}+{{x}_{1}}+{{x}_{3}}+{{x}_{2}}+{{x}_{3}}=0+2+\left( -6 \right) \\
& \Rightarrow 2\left( {{x}_{1}}+{{x}_{2}}+{{x}_{3}} \right)=-4 \\
& \Rightarrow \left( {{x}_{1}}+{{x}_{2}}+{{x}_{3}} \right)=-2...........\left( vii \right) \\
\end{align}$
Now , we will add the equations $\left( ii \right),\left( iv \right)$and $\left( vi \right)$.
On adding equations $\left( ii \right),\left( iv \right)$and $\left( vi \right)$, we get
$\begin{align}
& {{y}_{1}}+{{y}_{2}}+{{y}_{1}}+{{y}_{3}}+{{y}_{2}}+{{y}_{3}}=0+4+8 \\
& \Rightarrow 2\left( {{y}_{1}}+{{y}_{2}}+{{y}_{3}} \right)=12 \\
& \Rightarrow \left( {{y}_{1}}+{{y}_{2}}+{{y}_{3}} \right)=6...................\left( viii \right) \\
\end{align}$
Now , we know the coordinates of centroid of a triangle with vertices $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)$ is given as $\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$ .
So , the coordinates of centroid of $\Delta ABC$is
$G\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$
But , from equations $\left( vii \right)$and $\left( viii \right)$, we have
${{x}_{1}}+{{x}_{2}}+{{x}_{3}}=-2$ and ${{\text{y}}_{1}}+{{y}_{2}}+{{y}_{3}}=6\text{ }$
So , coordinates of the centroid of $\Delta ABC$are $G\left( \dfrac{-2}{3},2 \right)$ .
Hence , the statement $\left( 1 \right)$ is true.
Statement $2$: Let the vertices of triangle be $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)\And C\left( {{x}_{3}},{{y}_{3}} \right)$
So the midpoint of $AB$ is $D\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ , $\text{BC}$ is $\text{E}\left( \dfrac{{{x}_{2}}+{{x}_{3}}}{2},\dfrac{{{y}_{2}}+{{y}_{3}}}{2} \right)$ and $AC$ is $\text{F}\left( \dfrac{{{x}_{1}}+{{x}_{3}}}{2},\dfrac{{{y}_{1}}+{{y}_{3}}}{2} \right)$.
Now , we will find the centroid of $\Delta ABC$.
We know the coordinates of centroid of a triangle with vertices $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)$ is given as $\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$.
So , the centroid of $\Delta ABC$ is \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\] .
Now , we will find the centroid of $\Delta DEF$.
The centroid of $\Delta DEF$ is given as $\left( \dfrac{\dfrac{{{x}_{1}}+{{x}_{2}}}{2}+\dfrac{{{x}_{2}}+{{x}_{3}}}{2}+\dfrac{{{x}_{3}}+{{x}_{1}}}{2}}{3},\dfrac{\dfrac{{{y}_{1}}+{{y}_{2}}}{2}+\dfrac{{{y}_{3}}+{{y}_{2}}}{2}+\dfrac{{{y}_{1}}+{{y}_{3}}}{2}}{3} \right)$
$=\left( \dfrac{\dfrac{2\left( {{x}_{1}}+{{x}_{2}}+{{x}_{3}} \right)}{2}}{3},\dfrac{\dfrac{2\left( {{y}_{1}}+{{y}_{2}}+{{y}_{3}} \right)}{2}}{3} \right)$
$=\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$
= centroid of $\Delta ABC$.
Hence , the statement $\left( 2 \right)$ is true.
So , we can conclude that statement $\left( 1 \right)$ is true, statement $\left( 2 \right)$ is true and statement $\left( 2 \right)$ is a correct explanation for statement$\left( 1 \right)$.
So, (1) Statement $\left( 1 \right)$ is true, statement $\left( 2 \right)$ is true; statement $\left( 2 \right)$ is a correct explanation for statement $\left( 1 \right)$.
Note: The midpoint of line joining the points $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ is given as:
$\left( \dfrac{\left( {{x}_{1}}+{{x}_{2}} \right)}{2},\dfrac{\left( {{y}_{1}}+{{y}_{2}} \right)}{2} \right)$ and not $\left( \dfrac{\left( {{x}_{1}}-{{x}_{2}} \right)}{2},\dfrac{\left( {{y}_{1}}-{{y}_{2}} \right)}{2} \right)$ . Students often get confused between the two. Due to this confusion , they generally end up getting a wrong answer . So , such mistakes should be avoided .
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success
Master Class 12 Maths: Engaging Questions & Answers for Success
Master Class 12 Biology: Engaging Questions & Answers for Success
Master Class 12 Physics: Engaging Questions & Answers for Success
Master Class 8 Maths: Engaging Questions & Answers for Success
Class 8 Question and Answer - Your Ultimate Solutions Guide
Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE
10 examples of friction in our daily life
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE
1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE
Difference Between Prokaryotic Cells and Eukaryotic Cells
What are Quantum numbers Explain the quantum number class 11 chemistry CBSE