Question

State Pythagoras theorem.

Answer 1

Hint: This theorem is generally used with triangles possessing an ${{90}^{\circ }}$ angle at one of its vertices, and the side present opposite to that angle is called Hypotenuse while remaining are either base or height.

“Complete step-by-step answer:”
Here, we have a theorem which is a fundamental relation in Euclidean geometry among the three sides of a right triangle called Pythagoras’ theorem stated as,
It states that, “The area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides”.
This theorem can be written as an equation taking lengths of the sides of those squares as $a$ ,$b$ and $c$ respectively i.e.

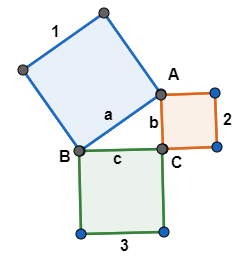
Here, as per the theorem,
Square 1 has side length = $a$; while square 2 has side length = $b$; and square 3 has side length = $c$, thus, the area of the square whose side is the hypotenuse ($a$) is equal to the sum of the areas of the squares on the other two sides ($b$) and ($c$), i.e.,
\[\Rightarrow {{a}^{2}}={{b}^{2}}+{{c}^{2}}...\text{ }\left( 1 \right)\],
Where,
$a$ = side $AB$= Hypotenuse;
$b$= side $AC$= Perpendicular;
$c$= side $BC$= Base;
and $\angle ACB={{90}^{\circ }}$.
Hence, as per the Pythagoras’ theorem for a triangle consisting of a right angle from equation (1) is
${{a}^{2}}={{b}^{2}}+{{c}^{2}}$

Note: Important point to keep in mind here is the proper selection of hypotenuse. As we know that Pythagoras’ theorem is not generally applied in any triangle but with a triangle consisting of ${{90}^{\circ }}$ angle. And hypotenuse is always a side opposite to that right-angled vertex of a triangle.