Question

State Biot-Savart Law. Derive an expression for this intensity of the magnetic field at the center of a current-carrying circular loop on its basis.

Answer 1

Hint: Biot-Savart law gives the magnetic field due to a current-carrying conductor. To find the intensity of the magnetic field at the center of a current-carrying circular loop, let us assume a circular conductor with radius $r$, carrying a current $I$.
Formula Used: $dB= \dfrac{\mu_{0}}{4\pi}\times \dfrac{Idlsin\theta}{r^{2}}$

Complete step-by-step solution:
Biot-Savart law states that the magnetic field produced at a point near a current-carrying conductor is proportional to the material of the medium $\mu_{0}$, the current $I$ flowing in the conductor, the small length of the wire \[dl\]involved, and inversely proportional to distance $r$ between the point and the conductor.
Mathematically, $dB \propto \mu_{0}$, $dB\propto I$, $dB \propto dl$ and $dB \propto \dfrac{1}{r^{2}}$
Then, $dB= \dfrac{\mu_{0}}{4\pi}\times \dfrac{Idlsin\theta}{r^{2}}$, where $\theta$ is the angle between\[dl\] and $r$.
Now to find the intensity of the magnetic field at the center of a current-carrying circular loop, let the radius of the circular conductor be $r$. Let a constant current $I$ flow through the loop, then
\[B=\int{dB=\dfrac{{{\mu }_{0}}}{4\pi }\times \int{\dfrac{Idl\sin \theta }{{{r}^{2}}}}}\]
Since the radius is always perpendicular to the tangent, we can say that \[dl\] and $r$ are perpendicular, $\theta=90^{\circ}$, i.e. $sin\theta=1$. Also the current $I$ and radius $r$ is a constant, we can take them out of the integral, then we get

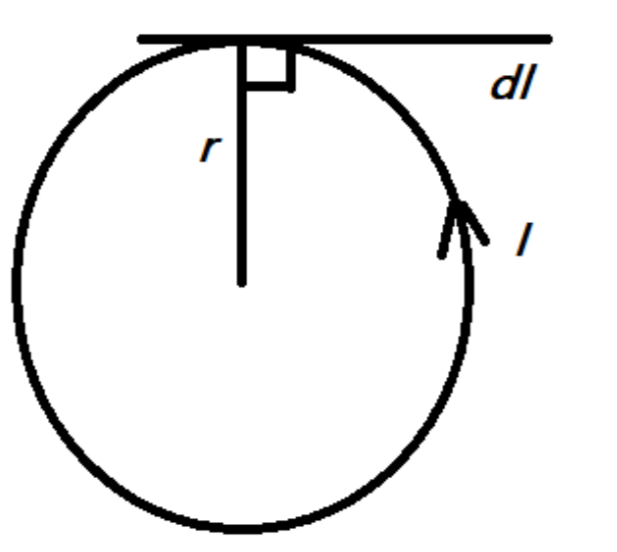
\[B=\int{dB=\dfrac{{{\mu }_{0}}I}{4\pi {{r}^{2}}}\times \int{dl}}\]
We know that the total length of the circle, which is the perimeter is given as $2\pi r$ i.e.\[dl=2\pi r\]
Then \[B=\dfrac{{{\mu }_{0}}I}{4\pi {{r}^{2}}}\times 2\pi r\]
\[=\dfrac{{{\mu }_{0}}I}{2r}\]
Hence the intensity of magnetic field \[B=\dfrac{{{\mu }_{0}}I}{2r}\]
Additional information:
The Biot-Savart law was the basis of magnetostatics and gives the relationship between the current and the magnetic field for any shape of conductor. It is expanded from the ampere's circuital law.

Note: From the formula, it is clear that the magnetic field produced depends on the nature of the conductor and the flow of current in the circuit. Note that, we are taking the cross product of the current and the small length, which is why we have a $\theta$ in the equation.