Question

State Biot-Savart law and then write it in vector form.

Answer 1

Hint: Biot-Savart law is the theory that derives a relation between a current carrying element and the magnetic field due to it at a point which is at a distance from the current carrying element. It is analogous to Coulomb’s law in electrostatics.

Complete answer:
Biot-Savart’s law in magnetostatics is important as Coulomb’s law is important to Electrostatics. Biot-Savart’s law deals with the moving charges that constitute a magnetic field at a point which is at a distance r from the element carrying the moving charges.
Consider an infinitesimal current carrying element ‘dl’ of a conductor. The magnetic field ‘dB’ produced by it is to be determined at a point P which is ‘r’ distance from the element. Let the current carrying element ‘dl’ be at an angle \[\theta \] with the displacement joining the point P, i.e., r.
Biot-Savart’s law states that the magnetic field at point P is proportional to the length of the element dl, the current flowing through it I and inversely proportional to the square of the distance r. The direction of the field is perpendicular to the plane containing both dl and r.
The magnetic field along the direction of dl is always zero.
                                            

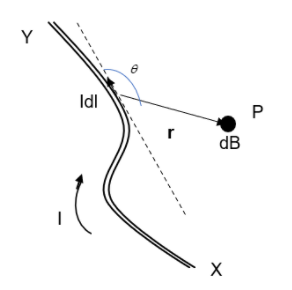
We can derive the formula for the Biot-Savart’s law as –
\[\begin{align}
  & d\mathbf{B}\propto \dfrac{Id\mathbf{l}\times \mathbf{r}}{{{r}^{3}}} \\
 & i.e.,\text{ d}\mathbf{B}\text{=}\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{Id\mathbf{l}\times \mathbf{r}}{{{r}^{3}}} \\
\end{align}\]
The above form gives the equation of Biot-Savart’s law in vector form.
The magnitude of the magnetic field is given by,
\[\begin{align}
  & \left| d\mathbf{B} \right|=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{Idl\sin \theta }{{{r}^{2}}} \\
 & \text{where},\text{ }\dfrac{{{\mu }_{0}}}{4\pi }={{10}^{-7}}Tm/A \\
\end{align}\]
The proportionality constant is the permeability of free space.
So, the required vector form of the law is –
\[\text{d}\mathbf{B}\text{=}\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{Id\mathbf{l}\times \mathbf{r}}{{{r}^{3}}}\]
And the direction of the magnetic field is perpendicular to both dl and r.

Note:
The magnetic field at the point is not just due to one point on the current carrying element. We have to integrate along the length of the conductor to find the total magnetic field at a point P. The right-hand thumb rule can give the direction of the magnetic field.