Question

Speed of flow of water in a river is 3 \[m{{s}^{-1}}\]. Speed of man in water is 5\[m{{s}^{-1}}\]. If the man wants to cross the river in the shortest time, then he has to head –
A) Normal to bank of river
B) \[{{37}^{0}}\]to the bank of the river.
C) \[{{53}^{0}}\]to the bank of river
D) Along the bank of the river

Answer 1

Hint: We know that swimming across a river where there is a flow can be done easier if we could adjust our path in the direction that will make possible the least time taking into consideration the given velocity of the river and the velocity at which we can swim.

Complete answer:
We know that to cross a river in which the water flows in a direction with a velocity, the swimmer needs to carefully align himself in the direction that will help him reach the other bank at the minimum possible time.
                                 

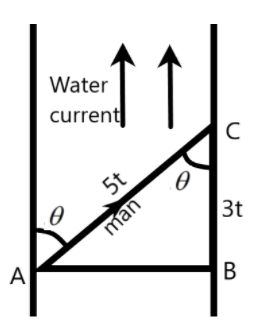
We can use the trigonometric relations to compute the path direction to be taken to reach the bank most quickly. Let ‘t’ be the shortest time taken by the man to reach the bank. The direction of the man can be given by the angle made with the bank \[\theta \] as –
\[\begin{align}
  & \text{In }\Delta \text{ABC,} \\
 & \cos \theta =\dfrac{BC}{AC} \\
 & \Rightarrow \cos \theta =\dfrac{3t}{5t} \\
 & \Rightarrow \cos \theta =0.6 \\
 & \Rightarrow \theta ={{\cos }^{-1}}(0.6) \\
 & \therefore \theta ={{53}^{0}} \\
\end{align}\]
The angle with which the man should swim is given above. If the man keeps an angle of \[{{53}^{0}}\] with the bank for crossing the river, then he can reach the other bank in the shortest time.
So, the required answer is with the angle of \[{{53}^{0}}\] with the bank.

The correct answer is option C.

Note:
We should understand that the man should tackle with the flow of the water as their directions are not the same. So, what we can do is to find the most comfortable path such that the effort and the time taken to swim can be reduced and therefore, he can safely cross the river.