Question

How do you solve \[\ln \left( x+1 \right)-\ln \left( x-2 \right)=\ln x\]?

Answer 1

Hint: Apply the formula: - \[\log m-\log n=\log \left( \dfrac{m}{n} \right)\] to simplify the L.H.S. Now, remove the log function from both the sides and cross – multiply the terms to form a quadratic equation in x. Solve this quadratic equation with the help of the discriminant formula: - \[x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\]. Here, a = coefficient of \[{{x}^{2}}\], b = coefficient of x and c = constant term. Reject the value of x that is invalid by using the information that the” argument of the log must be greater than 0”.

Complete step-by-step solution:
Here, we have been provided with the logarithmic equation: \[\ln \left( x+1 \right)-\ln \left( x-2 \right)=\ln x\] and we have been asked to solve it. That means we have to find the value of x.
Now, using the formula: - \[\log m-\log n=\log \left( \dfrac{m}{n} \right)\] in the L.H.S., we get,
\[\Rightarrow \ln \left( \dfrac{x+1}{x-2} \right)=\ln x\]
Comparing the argument of log on both the sides by removing the logarithmic function, we get,
\[\Rightarrow \dfrac{x+1}{x-2}=x\]
Cross – multiplying the terms, we get,
\[\begin{align}
  & \Rightarrow x+1=x\left( x-2 \right) \\
 & \Rightarrow x+1={{x}^{2}}-2x \\
 & \Rightarrow {{x}^{2}}-3x-1=0 \\
\end{align}\]
Assuming the coefficient of \[{{x}^{2}}\], coefficient of x and constant term as a, b and c respectively, we have,
\[\Rightarrow \] a = 1, b = -3, c = -1
Applying the discriminant formula given as: - \[x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\], we get,
\[\Rightarrow x=\dfrac{-\left( -3 \right)\pm \sqrt{{{\left( -3 \right)}^{2}}-4\left( 1 \right)\left( -1 \right)}}{2\times 1}\]
\[\Rightarrow x=\dfrac{3\pm \sqrt{13}}{2}\]
\[\Rightarrow x=\dfrac{3+\sqrt{13}}{2}\] or \[x=\dfrac{3-\sqrt{13}}{2}\]
Here, we have obtained two values of x. Now, let us check if any of the two values in invalid or not.
We know that a logarithmic function is only defined when its argument and base is greater than 0 and base is unequal to 1. In the above question we have ln, i.e., log to the base e, where the value of e is nearly 2.71 which is greater than 0. So, the base is defined. Now, let us define the argument. We have x, x + 1 and x – 2 as the arguments. So, we must have,
(i) \[x>0\Rightarrow x\in \left( 0,\infty \right)\]
(ii) \[x+1>0\Rightarrow x>-1\Rightarrow x\in \left( -1,\infty \right)\]
(iii) \[x-2>0\Rightarrow x>2\Rightarrow x\in \left( 2,\infty \right)\]
Since, we need to satisfy all the three conditions, therefore we must consider the intersection of the three sets of values of x obtained. So, we have,

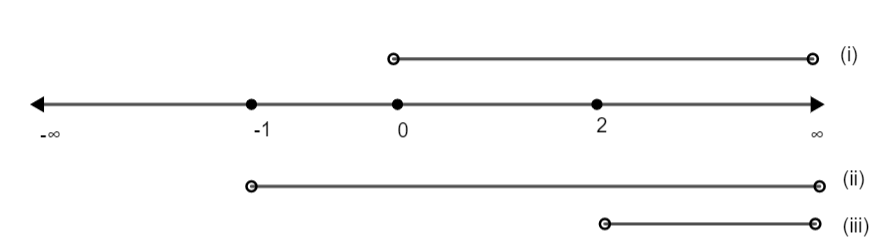
Therefore, \[x\in \left( 2,\infty \right)\] is the final condition.
Now, we can see that \[\dfrac{3-\sqrt{13}}{2}\] will be negative because \[\sqrt{13}\] is greater than 3, so \[x=\dfrac{3-\sqrt{13}}{2}\] does not satisfy the above condition. So, it must be rejected.
Hence, \[x=\dfrac{3+\sqrt{13}}{2}\] will be our answer.

Note: One may note that we cannot remove the log function directly from the initial expression: - \[\ln \left( x+1 \right)-\ln \left( x-2 \right)=\ln x\] as it will be a wrong approach. First, we need to convert the two logarithmic terms in the L.H.S. into a single logarithmic term in the L.H.S. into a single logarithmic term by using the difference to quotient rule and then only we can remove the function. Remember that we do not just have to calculate the value of x but we must check if it satisfies the domain or not. We must reject the invalid value as it makes the function undefined.