Question

How to solve \[2 \times \exp \left( x \right) + 2x - 7 = 0\]?

Answer 1

Hint:
Here, we will equate the given equation i.e. exponential equation and linear equation with zero separately, to find the solution of the equation. We will then plot the graph for these two equations and find the Point of intersection. The point of intersection is the solution for the given equation.

Complete step by step solution:
We are given with an equation \[2{e^x} + 2x - 7 = 0\]
Rewriting the given equation, we get
\[ \Rightarrow 2{e^x} = 7 - 2x\] …………………………………………………….\[\left( 1 \right)\]
Let us consider the function, \[f\left( x \right) = 2{e^x}\] and \[g\left( x \right) = 7 - 2x\]
Now, equating the function \[f\left( x \right)\] equals to zero, we get
\[2{e^x} = 0\]
Rewriting the equation, we get
\[ \Rightarrow {e^x} = \dfrac{0}{2}\]
\[ \Rightarrow {e^x} = 0\]
Now, by taking the exponential to the other side, we get
\[ \Rightarrow x = \log 0\]
Thus, \[x\] is not defined for the function \[f\left( x \right)\].
Now, equating the function \[g\left( x \right)\] equals to zero, we get
\[7 - 2x = 0\]
Adding \[2x\] on both the sides, we get
\[ \Rightarrow 2x = 7\]
Dividing both sides by 2, we get
\[ \Rightarrow x = \dfrac{7}{2}\]
Now, we will plot the graph for both the functions and we will find the point of intersection, we get

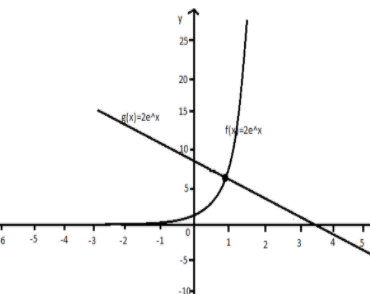
Therefore, the solution \[2 \times \exp \left( x \right) + 2x - 7 = 0\] is \[0.92\].

Note:
The given equation is a combination of an exponential equation and linear equation. So, it is quite impossible to solve the given equation easily. So, we should remember that these types of functions should be segregated and equated separately to find the solution or can be plotted into graphs to find the solution by pointing to the point of intersection of two functions, we will find the solution of the given equation. An exponential function is defined as a function in a variable written in exponents. A linear equation is defined as an equation with the highest degree as one.