Question

Six particles of mass $2\,kg$ are arranged at the corners of a regular hexagon of side $2\,m$. Find moment of inertia of the system about a given axis.
                

(1). $6$
(2). $24$
(3). $8$
(4). $16$

Answer 1

Hint: The system of particles is arranged on the vertices of a hexagon and the axis is such that it passes through two of the points. The distance of each particle from the axis must be calculated using properties of a hexagon and substitute it in the formula for moment of inertia to calculate moment of inertia. It is the product of mass and square of distance from the axis.
Formulas used:
$I=M{{R}^{2}}$
$\sin 60=\dfrac{AM}{AE}$

Complete answer:

The moment of inertia of a system about an axis is analogous to mass in translational motion. It is used to determine how much torque is required for an angular acceleration.
The moment of inertia is given by-
$I=M{{R}^{2}}$
Here, $I$ is the moment of inertia
$M$ is the mass of the system around the axis
$R$ is the distance from the axis
The axis is passing through one of the balls. So its distance from the axis is 0, hence its moment of inertia is zero

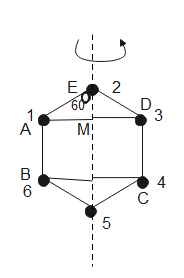
The axis passes through the particles on 2 and 5 so their distance from the axis is 0.
$\begin{align}
  & \Delta AEM \\
 & \sin 60=\dfrac{AM}{AE} \\
 & \Rightarrow \dfrac{\sqrt{3}}{2}=\dfrac{AM}{2} \\
 & \therefore AM=\sqrt{3} \\
\end{align}$
Therefore, the distance of particles at 1, 3, 4, 6 from the axis is $\sqrt{3}$.
From eq (1), the moment of inertia is calculated as-
$\begin{align}
  & I=M{{R}_{1}}^{2}+M{{R}_{2}}^{2}+M{{R}_{3}}^{2}+M{{R}_{4}}^{2}+M{{R}_{5}}^{2}+M{{R}_{6}}^{2} \\
 & I=2\times {{(\sqrt{3})}^{2}}+2\times 0+2\times {{(\sqrt{3})}^{2}}+2\times {{(\sqrt{3})}^{2}}+2\times 0+2\times {{(\sqrt{3})}^{2}} \\
 & \therefore I=24 \\
\end{align}$
Therefore, the moment of inertia of the whole system about the axis is $24$.

Hence, the correct option is (2).

Note:
The moment of inertia of rigid bodies is the sum of moment of inertia of all the point masses that make up the rigid body. If it were a continuous body instead of individual particles in the question, we could have used the theorem of perpendicular axes which states that the moment of inertia about a given axis is the sum of moment of inertia about two axes perpendicular to the given axis.