Question

Show that the minimum size of a plane mirror required to see the full image of an observer is half the size of that observer.

Answer 1

Hint: For an observer to observe the full image of himself in the mirror, the rays from the tip of the head and the ray from the bottom of his body (toe) must reflect from the mirror and reach his eyes. The angle between the reflected ray and incident ray for a mirror is equal. Draw the rays and accordingly in a triangle with equal angles, the corresponding sides are equal. Using this property, the problem can be solved.

Complete step by step solution:
We need to find the minimum size of the mirror required to see the full image of an observer. Let us consider an appropriate figure.

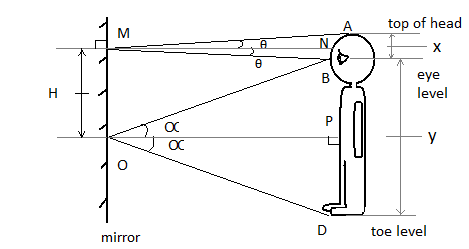
From the figure, we have the ray from the top of the head of the observer reflecting from the mirror and reaching his eyes. Similarly, the ray from the toe level is reaching the eye level after reflecting from the mirror.
We know that for a mirror, the angle of incidence is equal to the angle of reflection:
Therefore, in $\vartriangle AMB$ we have:
$\angle AMN = \angle BMN = \theta $
We know that length of sides opposite to equal angles are equal, therefore in $\vartriangle AMB$ , we can have:
$\angle AMN = \angle BMN$
$ \Rightarrow l\left( {AN} \right) = l\left( {BN} \right) = x$------equation $1$
We have assumed this length to be $x$ units.
Similarly, in $\vartriangle BOD$ we have:
$\angle BOP = \angle DOP = \alpha $
As, the length of sides opposite to equal angles are equal, therefore in $\vartriangle BOD$ , we can have:
$\angle BOP = \angle DOP$
$ \Rightarrow l\left( {BP} \right) = l\left( {PD} \right) = y$------- equation $2$
We have assumed this length to be $y$ units.
Now, from the figure it is clear that the total height of the man $h = 2(x + y)$ .
The size of the mirror $H$ is equal to the length is $BN + BP$ therefore, we have
$H = BN + BP$
From equation $1$ and equation $2$ , we can have
$H = \left( {x + y} \right)$
The ratio of the size of mirror to the height of the observer is given as:
$\dfrac{H}{h} = \dfrac{{\left( {x + y} \right)}}{{2\left( {x + y} \right)}}$
$ \Rightarrow H = \dfrac{h}{2}$
Thus, we have that the minimum size of the plane mirror required to see the full image of an observer is half the size of that observer.

Note: This result holds for any plane mirror and not for concave or convex mirrors. For any plane mirror, the angle of incidence is always equal to the angle of reflection. It must be noted that this result does not include the distance between the observer and the mirror. Thus, we can say that the size of mirror must be half irrespective of the distance between the observer and the mirror.