Show that the locus of the poles of chords which subtend a constant angle \[\alpha \] at the vertex is the curve \[{{\left( x+4a \right)}^{2}}=4{{\cot }^{2}}\alpha \left( {{y}^{2}}-4ax \right)\].
Answer
Verified360.3k+ views
Hint: The equation of chord joining the points \[\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[\left( at_{2}^{2},2a{{t}_{2}} \right)\] is given as \[\left( y-2a{{t}_{2}} \right)\left( {{t}_{1}}+{{t}_{2}} \right)=2\left( x-at_{2}^{2} \right)\], where \[{{t}_{1}}\] and \[{{t}_{2}}\] are parameters.
Complete step-by-step answer:
We will consider the equation of parabola to be \[{{y}^{2}}=4ax\].
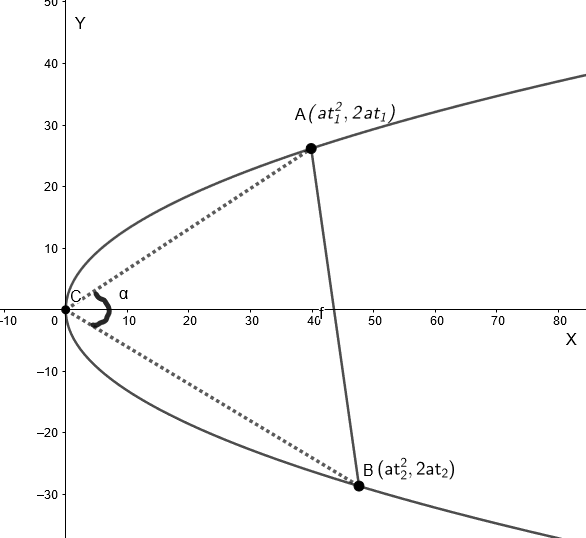
Now , we will consider two points on the parabola , given by \[A\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[B\left( at_{2}^{2},2a{{t}_{2}} \right)\], where \[{{t}_{1}}\] and \[{{t}_{2}}\] are parameters.
We know that the equation of line joining two points \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] is given as
\[\left( y-{{y}_{2}} \right)=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}\times \left( x-{{x}_{2}} \right)\]
So, the equation of the chord joining \[A\] and \[B\] is given as
\[\left( y-2a{{t}_{2}} \right)=\dfrac{\left( 2a{{t}_{2}}-2a{{t}_{1}} \right)}{\left( at_{2}^{2}-at_{1}^{2} \right)}\times \left( x-at_{2}^{2} \right)\]
\[\Rightarrow \left( y-2a{{t}_{2}} \right)=\dfrac{2a\left( {{t}_{2}}-{{t}_{1}} \right)}{a\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)}\times \left( x-at_{2}^{2} \right)\]
\[\Rightarrow \left( y-2a{{t}_{2}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)=2\left( x-at_{2}^{2} \right)....\left( i \right)\]
Now, we know the vertex of the parabola is at \[\left( 0,0 \right)\].
And we also know that the slope of line joining the points \[\left( {{x}_{1}},{{y}_{1}} \right)\]and\[\left( {{x}_{2}},{{y}_{2}} \right)\] is given by \[m=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}\].
So , the slope of the line joining \[A\] to vertex is given by
\[{{m}_{1}}=\dfrac{2a{{t}_{1}}-0}{at_{1}^{2}-0}\]
\[{{m}_{1}}=\dfrac{2}{{{t}_{1}}}\]
And the slope of the line joining \[B\] to vertex is given by
\[{{m}_{2}}=\dfrac{2a{{t}_{2}}-0}{at_{2}^{2}-0}\]
\[{{m}_{2}}=\dfrac{2}{{{t}_{2}}}\]
Now , we know if \[\theta \] is the angle between two lines with slope \[{{m}_{1}}\]and \[{{m}_{2}}\], then,
\[\tan \theta =\dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}}\]
Now, in the question it is given that the chord subtends angle \[\alpha \] at the vertex.
So, \[\tan \alpha =\dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}}......(ii)\]
Now , we will substitute the values of \[{{m}_{1}}\]and \[{{m}_{2}}\] in equation\[(ii)\].
On substituting the values of \[{{m}_{1}}\]and \[{{m}_{2}}\]in equation\[(ii)\], we get
\[\tan \alpha =\dfrac{\dfrac{2}{{{t}_{2}}}-\dfrac{2}{{{t}_{1}}}}{1+\dfrac{2}{{{t}_{2}}}\times \dfrac{2}{{{t}_{1}}}}\]
\[\Rightarrow \tan \alpha =\dfrac{2\left( {{t}_{1}}-{{t}_{2}} \right)}{{{t}_{1}}{{t}_{2}}+4}\]
\[\Rightarrow 2\left( {{t}_{1}}-{{t}_{2}} \right)=\tan \alpha \left( {{t}_{1}}{{t}_{2}}+4 \right)....\left( iii \right)\]
Now, we want to find the locus of the pole.
Let the pole be \[M\left( h,k \right)\].
We know, when the pole of a chord is \[\left( {{x}_{1}},{{y}_{1}} \right)\], then the equation of chord is given as
\[y{{y}_{1}}=2a\left( x+{{x}_{1}} \right)\]
Now, since \[\left( h,k \right)\] is the pole, so the equation of chord is given as
\[yk=2ax+2ah....\left( iv \right)\]
Now , we know the lines represented by equation \[\left( i \right)\] and equation \[\left( iv \right)\] are the same.
We also know that if two equations \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\] and \[{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\]are same then , \[\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}=\dfrac{{{c}_{1}}}{{{c}_{2}}}\]
Comparing equation \[\left( i \right)\]with equation \[\left( iv \right)\], we have
\[\dfrac{{{t}_{1}}+{{t}_{2}}}{k}=\dfrac{2}{2a}=\dfrac{2a{{t}_{1}}{{t}_{2}}}{2ah}\]
So , \[h=a{{t}_{1}}{{t}_{2}}\]and \[k=a\left( {{t}_{1}}+{{t}_{2}} \right).....\left( v \right)\]
Now, we know
\[{{t}_{1}}-{{t}_{2}}=\sqrt{{{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-4{{t}_{1}}{{t}_{2}}}\]
Substituting in \[\left( ii \right)\], we get
\[2\sqrt{{{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-4{{t}_{1}}{{t}_{2}}}=\tan \alpha \left( {{t}_{1}}{{t}_{2}}+4 \right).....\left( vi \right)\]
Substituting \[h=a{{t}_{1}}{{t}_{2}}\] and \[k=a\left( {{t}_{1}}+{{t}_{2}} \right)\] in equation \[\left( vi \right)\] we get
\[2\sqrt{{{\left( \dfrac{k}{a} \right)}^{2}}-\dfrac{4h}{a}}=\tan \alpha \left( \dfrac{h}{a}+4 \right)\]
\[\Rightarrow \dfrac{2}{a}\sqrt{{{k}^{2}}-4ah}=\dfrac{\tan \alpha }{a}\left( h+4a \right)\]
\[\Rightarrow 2\sqrt{{{k}^{2}}-4ah}=\tan \alpha \left( h+4a \right)\]
Squaring both sides, we get
\[4\left( {{k}^{2}}-4ah \right)={{\tan }^{2}}\alpha {{\left( h+4a \right)}^{2}}\]
\[\Rightarrow {{\left( h+4a \right)}^{2}}=4{{\cot }^{2}}\alpha \left( {{k}^{2}}-4ah \right)........(vii)\]
Now, to find the locus of \[M\left( h,k \right)\], we will substitute \[(x,y)\] in place of \[(h,k)\] in equation\[(vii)\].
So , the locus of \[M\left( h,k \right)\] is given as
\[{{\left( x+4a \right)}^{2}}=4{{\cot }^{2}}\alpha \left( {{y}^{2}}-4ax \right)\]
Note: : While simplifying the equations , please make sure that sign mistakes do not occur. These mistakes are very common and can cause confusions while solving. Ultimately the answer becomes wrong. So, sign conventions should be carefully taken .
Complete step-by-step answer:
We will consider the equation of parabola to be \[{{y}^{2}}=4ax\].
Now , we will consider two points on the parabola , given by \[A\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[B\left( at_{2}^{2},2a{{t}_{2}} \right)\], where \[{{t}_{1}}\] and \[{{t}_{2}}\] are parameters.
We know that the equation of line joining two points \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] is given as
\[\left( y-{{y}_{2}} \right)=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}\times \left( x-{{x}_{2}} \right)\]
So, the equation of the chord joining \[A\] and \[B\] is given as
\[\left( y-2a{{t}_{2}} \right)=\dfrac{\left( 2a{{t}_{2}}-2a{{t}_{1}} \right)}{\left( at_{2}^{2}-at_{1}^{2} \right)}\times \left( x-at_{2}^{2} \right)\]
\[\Rightarrow \left( y-2a{{t}_{2}} \right)=\dfrac{2a\left( {{t}_{2}}-{{t}_{1}} \right)}{a\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)}\times \left( x-at_{2}^{2} \right)\]
\[\Rightarrow \left( y-2a{{t}_{2}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)=2\left( x-at_{2}^{2} \right)....\left( i \right)\]
Now, we know the vertex of the parabola is at \[\left( 0,0 \right)\].
And we also know that the slope of line joining the points \[\left( {{x}_{1}},{{y}_{1}} \right)\]and\[\left( {{x}_{2}},{{y}_{2}} \right)\] is given by \[m=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}\].
So , the slope of the line joining \[A\] to vertex is given by
\[{{m}_{1}}=\dfrac{2a{{t}_{1}}-0}{at_{1}^{2}-0}\]
\[{{m}_{1}}=\dfrac{2}{{{t}_{1}}}\]
And the slope of the line joining \[B\] to vertex is given by
\[{{m}_{2}}=\dfrac{2a{{t}_{2}}-0}{at_{2}^{2}-0}\]
\[{{m}_{2}}=\dfrac{2}{{{t}_{2}}}\]
Now , we know if \[\theta \] is the angle between two lines with slope \[{{m}_{1}}\]and \[{{m}_{2}}\], then,
\[\tan \theta =\dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}}\]
Now, in the question it is given that the chord subtends angle \[\alpha \] at the vertex.
So, \[\tan \alpha =\dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}}......(ii)\]
Now , we will substitute the values of \[{{m}_{1}}\]and \[{{m}_{2}}\] in equation\[(ii)\].
On substituting the values of \[{{m}_{1}}\]and \[{{m}_{2}}\]in equation\[(ii)\], we get
\[\tan \alpha =\dfrac{\dfrac{2}{{{t}_{2}}}-\dfrac{2}{{{t}_{1}}}}{1+\dfrac{2}{{{t}_{2}}}\times \dfrac{2}{{{t}_{1}}}}\]
\[\Rightarrow \tan \alpha =\dfrac{2\left( {{t}_{1}}-{{t}_{2}} \right)}{{{t}_{1}}{{t}_{2}}+4}\]
\[\Rightarrow 2\left( {{t}_{1}}-{{t}_{2}} \right)=\tan \alpha \left( {{t}_{1}}{{t}_{2}}+4 \right)....\left( iii \right)\]
Now, we want to find the locus of the pole.
Let the pole be \[M\left( h,k \right)\].
We know, when the pole of a chord is \[\left( {{x}_{1}},{{y}_{1}} \right)\], then the equation of chord is given as
\[y{{y}_{1}}=2a\left( x+{{x}_{1}} \right)\]
Now, since \[\left( h,k \right)\] is the pole, so the equation of chord is given as
\[yk=2ax+2ah....\left( iv \right)\]
Now , we know the lines represented by equation \[\left( i \right)\] and equation \[\left( iv \right)\] are the same.
We also know that if two equations \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\] and \[{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\]are same then , \[\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}=\dfrac{{{c}_{1}}}{{{c}_{2}}}\]
Comparing equation \[\left( i \right)\]with equation \[\left( iv \right)\], we have
\[\dfrac{{{t}_{1}}+{{t}_{2}}}{k}=\dfrac{2}{2a}=\dfrac{2a{{t}_{1}}{{t}_{2}}}{2ah}\]
So , \[h=a{{t}_{1}}{{t}_{2}}\]and \[k=a\left( {{t}_{1}}+{{t}_{2}} \right).....\left( v \right)\]
Now, we know
\[{{t}_{1}}-{{t}_{2}}=\sqrt{{{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-4{{t}_{1}}{{t}_{2}}}\]
Substituting in \[\left( ii \right)\], we get
\[2\sqrt{{{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-4{{t}_{1}}{{t}_{2}}}=\tan \alpha \left( {{t}_{1}}{{t}_{2}}+4 \right).....\left( vi \right)\]
Substituting \[h=a{{t}_{1}}{{t}_{2}}\] and \[k=a\left( {{t}_{1}}+{{t}_{2}} \right)\] in equation \[\left( vi \right)\] we get
\[2\sqrt{{{\left( \dfrac{k}{a} \right)}^{2}}-\dfrac{4h}{a}}=\tan \alpha \left( \dfrac{h}{a}+4 \right)\]
\[\Rightarrow \dfrac{2}{a}\sqrt{{{k}^{2}}-4ah}=\dfrac{\tan \alpha }{a}\left( h+4a \right)\]
\[\Rightarrow 2\sqrt{{{k}^{2}}-4ah}=\tan \alpha \left( h+4a \right)\]
Squaring both sides, we get
\[4\left( {{k}^{2}}-4ah \right)={{\tan }^{2}}\alpha {{\left( h+4a \right)}^{2}}\]
\[\Rightarrow {{\left( h+4a \right)}^{2}}=4{{\cot }^{2}}\alpha \left( {{k}^{2}}-4ah \right)........(vii)\]
Now, to find the locus of \[M\left( h,k \right)\], we will substitute \[(x,y)\] in place of \[(h,k)\] in equation\[(vii)\].
So , the locus of \[M\left( h,k \right)\] is given as
\[{{\left( x+4a \right)}^{2}}=4{{\cot }^{2}}\alpha \left( {{y}^{2}}-4ax \right)\]
Note: : While simplifying the equations , please make sure that sign mistakes do not occur. These mistakes are very common and can cause confusions while solving. Ultimately the answer becomes wrong. So, sign conventions should be carefully taken .
Last updated date: 19th Sep 2023
•
Total views: 360.3k
•
Views today: 9.60k
