Question

Show that $ \left( 2,1 \right) $ is the circum-centre of the triangle formed by the vertices $ \left( 3,1 \right) $ , $ \left( 2,2 \right) $ and $ \left( 1,1 \right) $ .

Answer 1

Hint: We assume the circumcentre first and then find the distance from the vertices of a triangle which is equal and called the circum-radius. we equate those equations and find the solution for the assumed coordinates.

Complete step-by-step answer:
Let us assume that $ \left( h,k \right) $ is the circum-centre of the triangle formed by the vertices $ \left( 3,1 \right) $ , $ \left( 2,2 \right) $ and $ \left( 1,1 \right) $ .
We know that the distance of the circum-centre from the vertices of a triangle is equal and that is called the circum-radius.
Now for $ \left( h,k \right) $ , we can take its distance from the points $ \left( 3,1 \right) $ , $ \left( 2,2 \right) $ and $ \left( 1,1 \right) $ .
We will get 3 equations to solve the 2 unknowns of $ \left( h,k \right) $ .
We first find the general formula for distance between two arbitrary points.
We take two points $ \left( a,b \right) $ and $ \left( c,d \right) $ .
The formula for distance between those two points will be $ d=\sqrt{{{\left( a-c \right)}^{2}}+{{\left( b-d \right)}^{2}}} $ .
For our given points $ \left( h,k \right) $ and $ \left( 3,1 \right) $ , we put the values for $ a=h,c=3 $ and $ b=k,d=1 $ .
Therefore, the distance between those two points is $ r=\sqrt{{{\left( h-3 \right)}^{2}}+{{\left( k-1 \right)}^{2}}} $ .
For our given points $ \left( h,k \right) $ and $ \left( 2,2 \right) $ , we put the values for $ a=h,c=2 $ and $ b=k,d=2 $ .
Therefore, the distance between those two points is $ r=\sqrt{{{\left( h-2 \right)}^{2}}+{{\left( k-2 \right)}^{2}}} $ .
For our given points $ \left( h,k \right) $ and $ \left( 1,1 \right) $ , we put the values for $ a=h,c=1 $ and $ b=k,d=1 $ .
Therefore, the distance between those two points is $ r=\sqrt{{{\left( h-1 \right)}^{2}}+{{\left( k-1 \right)}^{2}}} $ .
 $ \begin{align}
  & r=\sqrt{{{\left( h-3 \right)}^{2}}+{{\left( k-1 \right)}^{2}}}=\sqrt{{{\left( h-2 \right)}^{2}}+{{\left( k-2 \right)}^{2}}} \\
 & \Rightarrow -6h-2k+10=-4h-4k+8 \\
 & \Rightarrow h-k=1...........(i) \\
\end{align} $
 $ \begin{align}
  & r=\sqrt{{{\left( h-1 \right)}^{2}}+{{\left( k-1 \right)}^{2}}}=\sqrt{{{\left( h-2 \right)}^{2}}+{{\left( k-2 \right)}^{2}}} \\
 & \Rightarrow -2h-2k+2=-4h-4k+8 \\
 & \Rightarrow h+k=3........(ii) \\
\end{align} $
We add these two equations and get
 $ \begin{align}
  & h-k+h+k=1+3 \\
 & \Rightarrow 2h=4 \\
 & \Rightarrow h=\dfrac{4}{2}=2 \\
\end{align} $
So, $ k=3-2=1 $ . The point becomes $ \left( 2,1 \right) $ .
Thus, proved $ \left( 2,1 \right) $ is the circum-centre of the triangle formed by the vertices $ \left( 3,1 \right) $ , $ \left( 2,2 \right) $ and $ \left( 1,1 \right) $ .

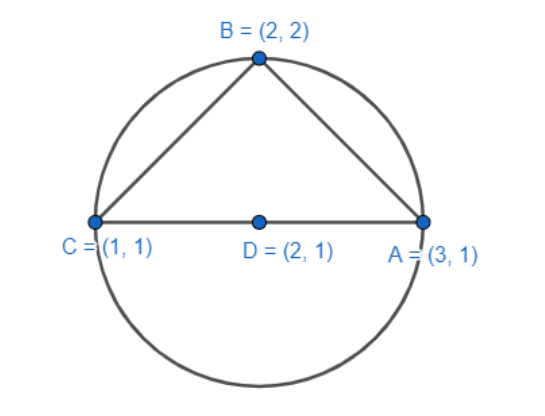
Note: The distance of the midpoint of the sides from the circumcentre is equal for all tree parts. We use that to find the coordinates of the point. The length of the sides will be considered in that way also. The triangle is actually a right-angle one.