Question

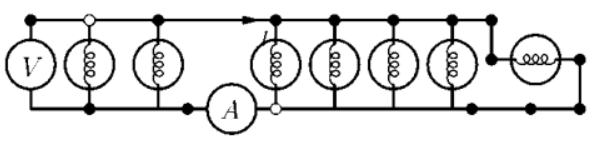
Seven identical lamps of resistance \[220\Omega \] each are connected to a 220V line as in the figure. Then the reading in the ammeter will be –

\[\begin{align}
  & A)\text{ 1}A \\
 & B)\text{ 2}A \\
 & C)\text{ 5}A \\
 & D)\text{ 7}A \\
\end{align}\]

Answer 1

Hint: We can find the equivalent resistance of the given circuit by analysing the type of circuit in which the lamps are connected. Once we know the equivalent resistance, we can calculate the current through any part of the circuit.

Complete answer:
The given circuit consists of seven lamps, all of which are of \[220\Omega \] each. On closer look, we understand that all the lamps are connected in parallel to each other. So, it is much easier now to calculate the equivalent resistance in the circuit.

\[\begin{align}
  & \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{R} \\
 & \dfrac{1}{{{R}_{eq}}}=\dfrac{7}{R} \\
 & \therefore {{R}_{eq}}=\dfrac{R}{7}=\dfrac{220}{7}\Omega \\
\end{align}\]
The current through the equivalent circuit is given by –
\[\begin{align}
  & {{I}_{eq}}=\dfrac{V}{{{R}_{eq}}} \\
 & \Rightarrow {{I}_{eq}}=\dfrac{220\times 7}{220}=7A \\
\end{align}\]
Now, let us have a look at the position of the ammeter, at which we have to find the current. We know that in a resistance combination, the current flows in different patterns. In a simple series circuit, all the elements will be fed with the same current. But in a parallel circuit, it is not true. The current gets divided among the resistors according to the resistances. So, in the present situation, we just need to find the current through the last five parallel elements.
The total current is given as 7A. Therefore, each of the resistors has a 1A current through it. The ammeter is placed in the path after 5 such resistors,
i.e.,
\[\therefore I=5\times 1=5A\]
is the reading on the ammeter.

The correct answer is option C.

Note:
For resistances with equal resistance connected in parallel combination, the resistance is given by dividing the value of each resistance by the number of resistors. For series combinations of equal resistors, we need to just multiply instead.