Question

What is the relative permittivity${{\varepsilon }_{r}}$ of oil in the given diagram?

Answer 1

Hint: As a first step, you could recall the coulomb’s law in terms of the relative permittivity of the medium. Now you could substitute the values as per the given condition in the question. After that, you could just compare or find the ratio of the two cases to get the final answer. Also remember, ${{\varepsilon }_{r}}$ for vacuum is 1.

Formula used: Coulomb’s law,
$F=\dfrac{1}{4\pi {{\varepsilon }_{0}}{{\varepsilon }_{r}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}$

Complete step by step answer:
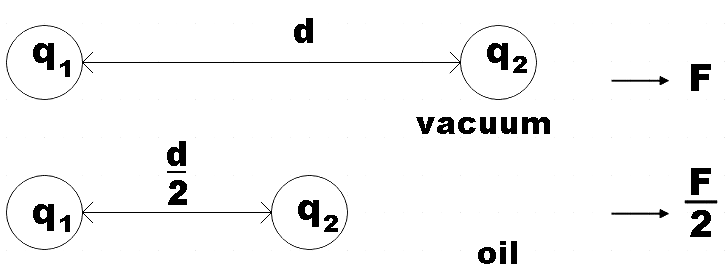
In the question, we are given two charges that is kept in two different medium at different distance and we are asked find the relative permittivity of oil, ${{\varepsilon }_{r}}$
In order to solve the given question we could use the coulomb’s law. Coulomb’s law states that the magnitude of electrostatic force (be it attractive or repulsive) between two charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. That is, if ${{q}_{1}}$and ${{q}_{2}}$ were the two charges and r the distance between them, then,
$F\propto \dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}$
$\Rightarrow F=k\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}$ …………………………….. (1)
Here, $k=\dfrac{1}{4\pi \varepsilon }$
Where,$\varepsilon $ is the permittivity of the medium in which the charges are kept. But,
${{\varepsilon }_{r}}=\dfrac{\varepsilon }{{{\varepsilon }_{0}}}$
$\Rightarrow \varepsilon ={{\varepsilon }_{0}}{{\varepsilon }_{r}}$
Where,${{\varepsilon }_{0}}$ is the absolute permittivity and ${{\varepsilon }_{r}}$ is the relative permittivity of the medium
Substituting in (1), we get,
$F=\dfrac{1}{4\pi {{\varepsilon }_{0}}{{\varepsilon }_{r}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}$
Now let us consider the first case where the charges are d distance apart in vacuum. There the coulomb’s law will be given by, ${{\varepsilon }_{r}}$ for vacuum is 1,
$F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{d}^{2}}}$…………………………………….. (2)
Coulomb’s law for the second case where the same charges are kept at$\dfrac{d}{2}$ distance apart in oil of relative permittivity ${{\varepsilon }_{r}}$ is given by,
$\dfrac{F}{2}=\dfrac{1}{4\pi {{\varepsilon }_{0}}{{\varepsilon }_{r}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{\left( \dfrac{d}{2} \right)}^{2}}}$ …………………………………….. (3)
Dividing (2) by (3) gives,
$\dfrac{F}{\dfrac{F}{2}}=\dfrac{\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{d}^{2}}}}{\dfrac{1}{4\pi {{\varepsilon }_{0}}{{\varepsilon }_{r}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{\left( \dfrac{d}{2} \right)}^{2}}}}$
$\Rightarrow 2=\dfrac{{{\varepsilon }_{r}}}{4}$
$\therefore {{\varepsilon }_{r}}=8$

Therefore, we found the relative permittivity of oil is found to be 8.

Note: We have used the permittivity of free space or absolute permittivity $\left( {{\varepsilon }_{0}} \right)$while solving the question. It is actually considered as the permittivity of vacuum or air and its value is given by,
${{\varepsilon }_{0}}=8.854\times {{10}^{-12}}{{C}^{2}}{{N}^{-1}}{{m}^{-2}}$
So the relative permittivity, which is the permittivity of the medium relative to that of vacuum will obviously be 1 for vacuum.
${{\varepsilon }_{r}}=\dfrac{{{\varepsilon }_{0}}}{{{\varepsilon }_{0}}}=1$