Question

What is the relationship between critical angle and refractive index?
\[
  {\text{A}}{\text{. }}\dfrac{1}{{\sin {i_{\text{c}}}}} = \mu \\
  {\text{B}}{\text{. }}\sin {i_{\text{c}}} = \mu \\
  {\text{C}}{\text{. }}\sin {i_{\text{c}}} \times \dfrac{1}{\mu } \\
 \]
${\text{D}}{\text{.}}$ All

Answer 1

Hint: Here, we will proceed by using Snell's law and then we will put the conditions for critical angle to this law and find the required relationship between critical angle and refractive index.

Complete step-by-step answer:

Formulas Used- $\dfrac{{\sin i}}{{\sin r}} = \dfrac{{{\mu _{\text{a}}}}}{{{\mu _{\text{b}}}}}$ and $\sin {90^0} = 1$.

Let us suppose a light ray is incident from a rarer medium I having refractive index of ${\mu _{\text{a}}}$ and this light ray gets refracted into a denser medium II having refractive index of ${\mu _{\text{b}}}$. Here, refraction will be occurring.

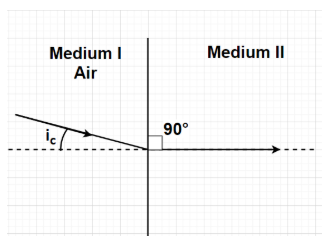
According to Snell’s law (or second law of refraction), for a light ray entering from a medium with refractive index ${\mu _{\text{a}}}$ to a medium with refractive index ${\mu _{\text{b}}}$ along with the angle of incidence as i and the angle of refraction as r, we can write

$\dfrac{{\sin i}}{{\sin r}} = \dfrac{{{\mu _{\text{a}}}}}{{{\mu _{\text{b}}}}}{\text{ }} \to {\text{(1)}}$

As the incidence angle in any medium approaches a certain critical value, the refracted ray lies along the boundary, having a refractive angle of 90 degrees. This angle of incidence is known as the critical angle. It is the highest angle of incidence for which there might still be refraction.

For critical angle (${i_{\text{c}}}$), Angle of incidence i = Critical angle ${i_{\text{c}}}$ and Angle of refraction r = ${90^0}$
Now, replacing i by ${i_{\text{c}}}$ and r by ${90^0}$ in the formula given by equation (1), we get

$\dfrac{{\sin {i_{\text{c}}}}}{{\sin {{90}^0}}} = \dfrac{{{\mu _{\text{a}}}}}{{{\mu _{\text{b}}}}}$
Using $\sin {90^0} = 1$ in the above equation, we get

$
   \Rightarrow \dfrac{{\sin {i_{\text{c}}}}}{1} = \dfrac{{{\mu _{\text{a}}}}}{{{\mu _{\text{b}}}}} \\
   \Rightarrow \sin {i_{\text{c}}} = \dfrac{{{\mu _{\text{a}}}}}{{{\mu _{\text{b}}}}}{\text{ }} \to {\text{(2)}} \\
 $

Now, assuming the rarer medium be air which has a refractive index of 1 (i.e., ${\mu _{\text{a}}} = 1$) and the denser medium has a refractive index of $\mu $ (i.e., $\mu = {\mu _{\text{b}}}$)

By putting ${\mu _{\text{a}}} = 1$ and $\mu = {\mu _{\text{b}}}$ in equation (2), we get
$ \Rightarrow \sin {i_{\text{c}}} = \dfrac{1}{\mu }$

The above equation represents the required relationship between critical angle and refractive index.

Hence, option C is correct.

Note: The refractive index is the ratio of speed of light in medium to the speed of light in vacuum. As light travels in a medium other than vacuum, the medium's atoms continually absorb and re-emit the light particles, slowing down the speed of light. Refractive index is also called a refraction index, measuring the bending of a ray of light as it travels from one medium to another.