Question

Relation between coefficient of static friction ${{\text{ }\!\!\mu\!\!\text{ }}_{\text{S}}}$ and the angle of friction is
 $\begin{align}
  & \text{a) }{{\text{ }\!\!\mu\!\!\text{ }}_{\text{S}}}\text{=sin }\!\!\theta\!\!\text{ } \\
 & \text{b) }{{\text{ }\!\!\mu\!\!\text{ }}_{\text{S}}}\text{=cos }\!\!\theta\!\!\text{ } \\
 & \text{c) }{{\text{ }\!\!\mu\!\!\text{ }}_{\text{S}}}\text{=tan }\!\!\theta\!\!\text{ } \\
 & \text{d) None of these} \\
\end{align}$

Answer 1

Hint: To obtain the relation between coefficient of friction and the angle of friction we need to know how we define the following. The coefficient to friction is basically responsible for frictional force that holds the body at rest. The angle of friction is defined as the angle between the resultant of the normal and the frictional force and the normal force of a body on ground. Now to obtain the relation, first we have drawn the diagram and using trigonometric definition we can obtain the required result.

Complete step-by-step answer:
To begin with let us consider a body of mass m resting on the ground as shown in the fig below.

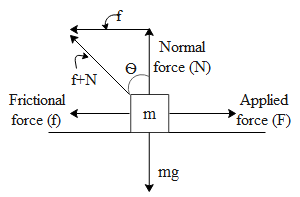
Let us say we applied a force F on the body at rest. The body will still be at rest due to the frictional force. At one point the frictional force will be equal to the applied force at equilibrium. The frictional force at this point is equal to ${{\text{ }\!\!\mu\!\!\text{ }}_{\text{S}}}$ times the normal force. This can mathematically be represented as,
$\begin{align}
  & \text{f =}{{\text{ }\!\!\mu\!\!\text{ }}_{\text{S}}}\text{N} \;\;\;\;\;\;\;\text{Since N=mg} \\
 & \text{f =}{{\text{ }\!\!\mu\!\!\text{ }}_{\text{S}}}\text{mg} \\
\end{align}$
If we see in the above diagram the angle between the resultant i.e. of( frictional force and the normal force)and the normal force is denoted by $\text{ }\!\!\theta\!\!\text{ }$. Now as we wish to calculate this angle let us write the parallel vector of frictional force to the head of the normal vector. Since the normal and the frictional force are perpendicular to each other by trigonometric definition of $\text{tan }\!\!\theta\!\!\text{ }$
We get,
$\text{tan }\!\!\theta\!\!\text{ }=\dfrac{\text{f}}{\text{N}}$ Since, $\text{f =}{{\text{ }\!\!\mu\!\!\text{ }}_{\text{S}}}\text{mg}$ and N= mg,

$\text{tan }\!\!\theta\!\!\text{ }=\dfrac{{{\text{ }\!\!\mu\!\!\text{ }}_{\text{S}}}\text{mg}}{\text{mg}}={{\text{ }\!\!\mu\!\!\text{ }}_{\text{S}}}$.

So, the correct answer is “Option C”.

Note:
It is to be noted the numerical value of angle of friction and the angle of repose is the same. The angle of repose is the angle between the resultant of the normal and the frictional force, and the normal force of a body on ground. If we observe this definition it is the same as the angle of friction but the difference is that the body itself is on an inclined surface and not horizontal surface.