Question

Rain is falling vertically with a speed of 35 m/s. Wind start blowing after sometime
with a speed of 12 m/s in east to west direction. In which direction should a boy waiting at a
Does the bus stop hold his umbrella?

Answer 1

Hint:The direction of the rain gets affected by the wind speed and the boy should hold the umbrella opposite to the direction of the resultant of the velocity of the rain and the velocity of the wind.

Complete step by step answer:
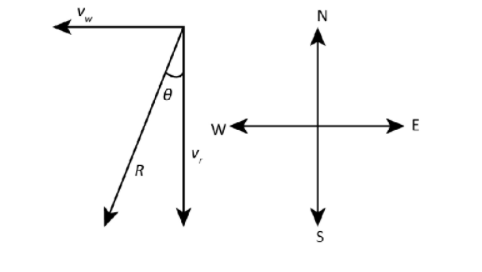
From the given question, we know that the velocity of rain vertically
downwards,${\overrightarrow v _r} = - 35\,\mathop {\rm{j}}\limits^ \wedge
{\rm{m}}{{\rm{s}}^{ - 1}}$ and the velocity of the wind, ${\overrightarrow v _w} = - 12\mathop
{\rm{i}}\limits^ \wedge \;{\rm{m}}{{\rm{s}}^{ - 1}}$

The rain will drop in the direction of the resultant velocity of the rain and the velocity of the wind.

We know that the direction of the resultant is calculated as,
$\tan \theta = \dfrac{{{v_w}}}{{{v_r}}}$
Substitute the given values in the above equation, we get,
$
\tan \theta = \dfrac{{12}}{{35}}\\
\theta = {\tan ^{ - 1}}\left( {\dfrac{{12}}{{35}}} \right)\\
= 18.92^\circ
$

Thus, a boy waiting at a bus stop holds his umbrella in the opposite direction of the resultant
velocity of the rain in order to protect from rain drops and he must hold the umbrella in the direction 18.92 degree south of west.

Note:There is another method to calculate the direction of the resultant of the rain that is $\left( {90^\circ - 18.92^\circ } \right) = 71.08^\circ $ or it can be calculated as $\tan \theta = \dfrac{{{v_r}}}{{{v_w}}}$ and in this case, the boy must be hold the umbrella in the direction 71.08 degree west of south. Be extra careful while determining the direction of the resultant rain drops, there is a high chance of making a mistake.