Question

Radius of curvature of convex mirror is 40cm and the size of the object is twice as that of the image, then the image distance is
A. 60cm
B. 20cm
C. 40cm
D. 30cm

Answer 1

Hint: From the given radius of curvature, you could find the focal length. Now recall the expressions for magnification and then apply the given condition on height of image and object and thus get the relation between image distance and object distance. Now you could substitute the same along with the focal length in mirror formula and hence get the image distance.
Formula used:
Mirror formula,
$\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$

Complete answer:
In the question we are given a convex lens whose radius of curvature is 40cm. We are also told that the size of the object is twice as that of the image and then we are asked to find the image distance using this information.

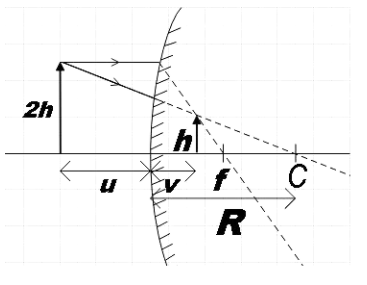
We know that the radius of curvature of a mirror is twice the focal length of the mirror. Therefore,
$R=2f$
Also, as the given mirror is convex, the radius of curvature is positive. So, the focal length given mirror will be,
$f=\dfrac{R}{2}$
$\Rightarrow f=\dfrac{40}{2}$
$\therefore f=20cm$ ……………………………………….. (1)
We know that magnification of a mirror can be given by two expressions: one in terms of height of image $\left( {{h}_{i}} \right)$ and object$\left( {{h}_{o}} \right)$ and the other in terms of object distance (u) and image distance (v).$m=\dfrac{{{h}_{i}}}{{{h}_{o}}}$
$m=-\dfrac{v}{u}$
Combining the two equations we get,
$\dfrac{{{h}_{i}}}{{{h}_{o}}}=-\dfrac{v}{u}$ ……………………………….. (2)
But we are given,
${{h}_{o}}=2{{h}_{i}}$
Now (2) becomes,
$\dfrac{{{h}_{i}}}{2{{h}_{i}}}=-\dfrac{v}{u}$
But u is negative for convex mirrors.
$\Rightarrow \dfrac{1}{2}=-\dfrac{v}{-u}$
$\therefore u=2v$ ………………………………………. (3)
Now, recall the mirror formula given by,
$\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$
But as u is negative for convex mirror,
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$
$\Rightarrow f=\dfrac{uv}{u-v}$
Substituting (1) and (3),
$20=\dfrac{2{{v}^{2}}}{2v-v}$
$\Rightarrow v=\dfrac{20}{2}$
$\therefore v=10cm$
Therefore, we found the image distance of the given convex mirror to be,
$v=10cm$

Hence, option A is the correct answer.

Note:
In optics, the most fundamental part of solving numerical problems is getting the sign conventions right while substituting. We normally use the pole of the mirror (the point of the mirror that is on the principal axis) as the reference point while taking measurements. All the measurements made from pole to the left are taken negative and those to the right of pole are taken positive.