Question

Prove that $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x} = 1$ ( $x$ being measured in radians).

Answer 1

Hint: Sandwich theorem is useful in proving the limits given in the question.
Theorem: Sandwich Theorem:
Let \[f,g\] and $h$ be real functions such that $g\left( x \right) \leqslant f\left( x \right) \leqslant h\left( x \right)$ for all $x$ in the common domain of definition.
For some limit $a$, if \[\mathop {\lim }\limits_{x \to a} g\left( x \right) = l = \mathop {\lim }\limits_{x \to a} h\left( x \right)\], then \[\mathop {\lim }\limits_{x \to a} f\left( x \right) = l\]. This can be illustrated as the following:

Try to prove the inequality relating to trigonometric functions. $\cos x < \dfrac{{\sin x}}{x} < 1$, and the given limit can be easily proved by the sandwich theorem.

Complete step by step answer:
Step 1: Prove the inequality $\cos x < \dfrac{{\sin x}}{x} < 1$
Consider figure 1.

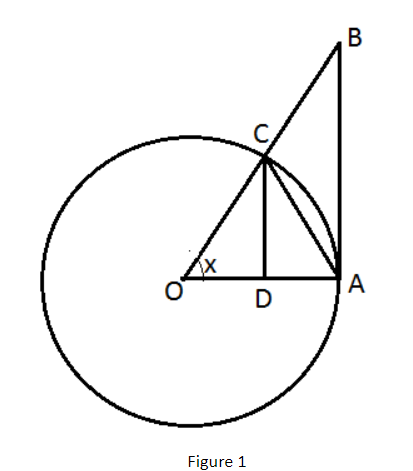
In figure 1, O is the center of the unit circle such that the angle $\angle AOC$ is $x$ radians and $0 < x < \dfrac{\pi }{2}$.
Line segment BA and CD are perpendicular to OA.
Further, join AC. Then
Area of $\vartriangle AOC$ < area of sector $OAC$ < area of $\vartriangle AOB$
The area of a triangle is half of the product of base and height.
Area of a sector of a circle = $\dfrac{\theta }{{2\pi }}\left( {\pi {r^2}} \right)$, where $\theta $ is the angle of the sector.
$ \Rightarrow \dfrac{1}{2}OA.CD < \dfrac{x}{{2\pi }}\pi {\left( {OA} \right)^2} < \dfrac{1}{2}OA.AB$
$ \Rightarrow CD < x\left( {OA} \right) < AB$ …… (1)
In $\vartriangle OCD$
$\sin x = \dfrac{{{\text{perpendicular}}}}{{{\text{hypotenuse}}}}$
Therefore, $\sin x = \dfrac{{CD}}{{OC}}$
The line segments OC and OA are the radius of the circle with center O in figure 1.
Thus, OC = OA
Therefore, $\sin x = \dfrac{{CD}}{{OA}}$
Hence, $CD = OA\sin x$
In $\vartriangle AOB$
$\tan x = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}$
Therefore, $\tan x = \dfrac{{AB}}{{OA}}$
Hence, $AB = OA\tan x$
Put the values of CD and AB in the inequality (1)
$ \Rightarrow OA\sin x < x\left( {OA} \right) < OA\tan x$
We know $\tan x = \dfrac{{\sin x}}{{\cos x}}$
\[ \Rightarrow \sin x < x < \dfrac{{\sin x}}{{\cos x}}\]
Dividing throughout by $\sin x$, we get:
\[ \Rightarrow 1 < \dfrac{x}{{\sin x}} < \dfrac{1}{{\cos x}}\]
Take reciprocals throughout, we have:
$ \Rightarrow \cos x < \dfrac{{\sin x}}{x} < 1$

Step 2: Use sandwich theorem to prove the given limit
We know that $\mathop {\lim }\limits_{x \to a} \cos \left( {f\left( x \right)} \right) = \cos \mathop {\lim }\limits_{x \to a} \left( {f\left( x \right)} \right)$
Thus, the \[\mathop {\lim }\limits_{x \to 0} \cos x = \cos \mathop {\lim }\limits_{x \to 0} \left( x \right)\]
Therefore, $\cos 0 = 1$
Hence, $\mathop {\lim }\limits_{x \to 0} \cos x = 1$
And $\mathop {\lim }\limits_{x \to 1} 1 = 1$
We have, $\mathop {\lim }\limits_{x \to 0} \cos x = 1 = \mathop {\lim }\limits_{x \to 0} 1$
Then $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x} = 1$ by the sandwich theorem.

The limit $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x} = 1$ has been proved.

Note:
Use the above limit $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x} = 1$ for future questions. For example:
Evaluate: $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin 4x}}{{\sin 2x}}$
Multiplying and dividing by $4x$ and make the angles in the sine function and dividing angle the same.
\[ \Rightarrow \mathop {\lim }\limits_{x \to 0} \left[ {\dfrac{{\sin 4x}}{{4x}} \times \dfrac{{2x}}{{\sin 2x}} \times 2} \right]\]
\[
   \Rightarrow \mathop {\lim }\limits_{x \to 0} \dfrac{{\sin 4x}}{{4x}} \times \mathop {\lim }\limits_{x \to 0} \left[ {\dfrac{1}{{\dfrac{{\sin 2x}}{{2x}}}}} \right] \times \mathop {\lim }\limits_{x \to 0} 2 \\
   \Rightarrow \mathop {\lim }\limits_{x \to 0} \dfrac{{\sin 4x}}{{4x}} \times \left[ {\dfrac{{\mathop {\lim }\limits_{x \to 0} 1}}{{\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin 2x}}{{2x}}}}} \right] \times \mathop {\lim }\limits_{x \to 0} 2 \\
   \Rightarrow 1 \times \dfrac{1}{1} \times 2 \\
   \Rightarrow 2 \\
 \]