
Poor Dolly’s T.V. has only 4 channels, all of them quite boring. Hence, it is not surprising that she desires to switch (change) channels after every one minute. Then, find the number of ways in which she can change the channels so that she is back to her original channel for the first time after 4 min.
Answer
541.8k+ views
Hint: In the solution of this question, we are going to use the techniques of permutation and combination for solving. First, we will find the choices of switching channels from the first channel to the next three channels. After that, we will find the choices of switching channels from any of those three channels to any two channels. From here, we will find the choices for switching the rest channels and get the answer.
Complete step by step answer:
Let us solve this question.
In this question it is given that the T.V. of Dolly has only 4 channels. And, she changes the channels after every one minute. We have to find the number of ways in which she can change the channels so that she is back to her original or initial channel for the first time. That means she is changing the 4 channels after every one minute and coming back to the initial channel for the first time. So, we have to find the number of ways of changing the channels and coming back to the channel from where she started switching.
So, let us say that the channels A, B, C, and D.
The first channel is A and the last channel is D.
When she starts switching from channel A, she has 3 choices (that are channels B, C, and D) for switching. Before switching from A, she has 4 minutes. Now, she has 3 minutes after switching from A.
Here, we get the choices as 3.
Now, suppose she has reached a channel (any of B, C, and D), and now she is going to switch from those 3 channels to the rest 2 channels, then she will have only 2 choices. (Suppose, she has reached the channel B, then she will have only channels C and D for switching, so she will only have two choices)
We cannot choose channel A, we have to reach channel A after 4 minutes for the first time.
From here, we get 2 choices.
Now, she has 2 minutes to switch.
Now, she has switched any of 2 channels. Suppose, she has chosen C from the channels C and D. Then, for switching the next channel, she will have only 2 choices. (Suppose, she is in channel B, then she has 2 channels that are C and D to switch.)
From here, we get 2 choices.
Now, she has only one minute for switching. In the last minute, she will switch to A and it will have only one choice.
From here, we get only one choice.
Therefore, total choices or ways in which she will change the channels so that she is back to her original channel for the first time after 4 minutes will be
\[3\times 2\times 2\times 1=12\]
Note: As we can see that this question is from the topic of permutation and combination, so we should have a better knowledge in that topic. Don’t forget that, she cannot go to the first channel before completing the 4 minutes.
We can understand the solution from a different method.
Drawing the tree diagram for switching the channels, we get
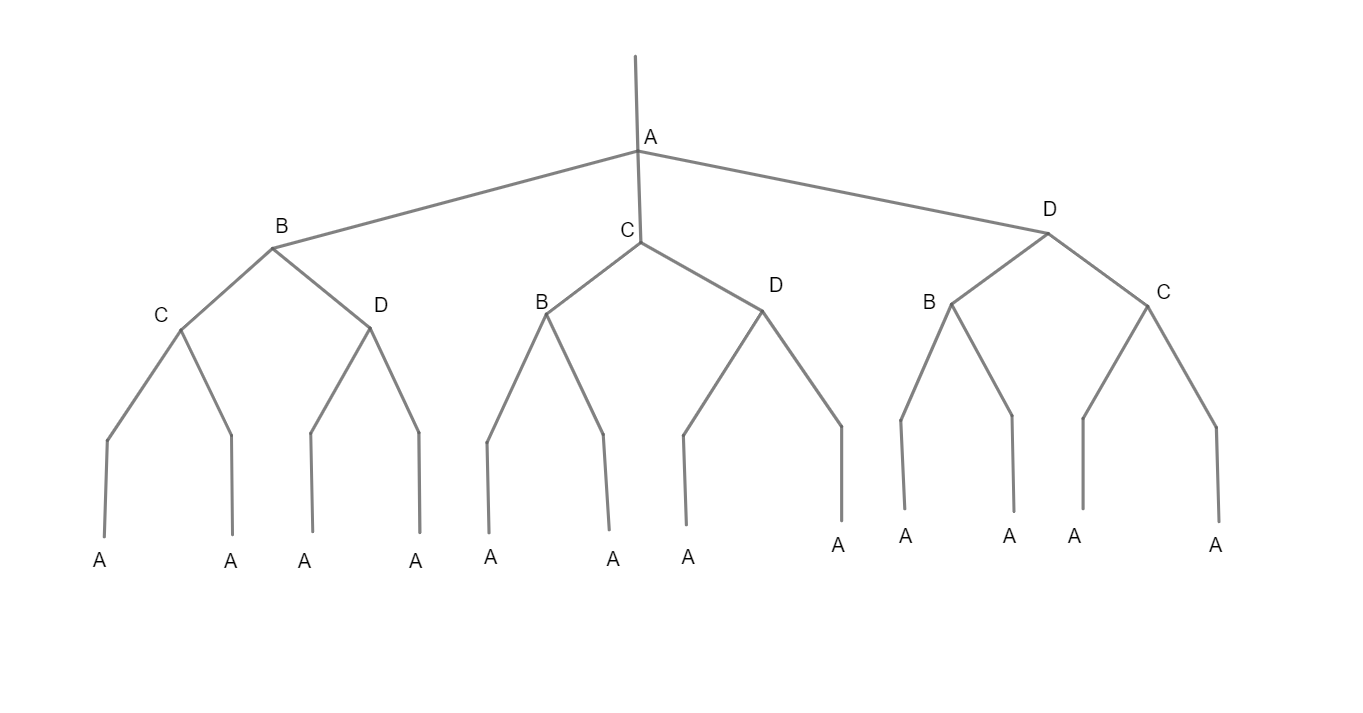
Methods of solving are the same but we have used here a tree diagram.
From here, we can see that there are 12 ways.
Complete step by step answer:
Let us solve this question.
In this question it is given that the T.V. of Dolly has only 4 channels. And, she changes the channels after every one minute. We have to find the number of ways in which she can change the channels so that she is back to her original or initial channel for the first time. That means she is changing the 4 channels after every one minute and coming back to the initial channel for the first time. So, we have to find the number of ways of changing the channels and coming back to the channel from where she started switching.
So, let us say that the channels A, B, C, and D.
The first channel is A and the last channel is D.
When she starts switching from channel A, she has 3 choices (that are channels B, C, and D) for switching. Before switching from A, she has 4 minutes. Now, she has 3 minutes after switching from A.
Here, we get the choices as 3.
Now, suppose she has reached a channel (any of B, C, and D), and now she is going to switch from those 3 channels to the rest 2 channels, then she will have only 2 choices. (Suppose, she has reached the channel B, then she will have only channels C and D for switching, so she will only have two choices)
We cannot choose channel A, we have to reach channel A after 4 minutes for the first time.
From here, we get 2 choices.
Now, she has 2 minutes to switch.
Now, she has switched any of 2 channels. Suppose, she has chosen C from the channels C and D. Then, for switching the next channel, she will have only 2 choices. (Suppose, she is in channel B, then she has 2 channels that are C and D to switch.)
From here, we get 2 choices.
Now, she has only one minute for switching. In the last minute, she will switch to A and it will have only one choice.
From here, we get only one choice.
Therefore, total choices or ways in which she will change the channels so that she is back to her original channel for the first time after 4 minutes will be
\[3\times 2\times 2\times 1=12\]
Note: As we can see that this question is from the topic of permutation and combination, so we should have a better knowledge in that topic. Don’t forget that, she cannot go to the first channel before completing the 4 minutes.
We can understand the solution from a different method.
Drawing the tree diagram for switching the channels, we get

Methods of solving are the same but we have used here a tree diagram.
From here, we can see that there are 12 ways.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
Differentiate between an exothermic and an endothermic class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

What is boron A Nonmetal B Metal C Metalloid D All class 11 chemistry CBSE

Bond order ofO2 O2+ O2 and O22 is in order A O2 langle class 11 chemistry CBSE

Distinguish between verbal and nonverbal communica class 11 english CBSE




