Question

When the point of suspension of pendulum is moved, its period of oscillation
A. decreases when it moves vertically upwards with an acceleration a
B. decrease when it moves vertically upwards with an acceleration greater than 2g
C. increase when it moves horizontal with acceleration a
D. all of the above

Answer 1

Hint: One could read the question and then consider each of the given options one by one. You could make a free body diagram for each of the three cases and work accordingly. You could also make use of the expression for the time period of oscillation to make the conclusion in each case.

Formula used:
Time period of oscillation,
$T=2\pi \sqrt{\dfrac{l}{{{g}_{eff}}}}$

Complete step-by-step solution:
In the question, we are given a condition that the point of suspension of a simple pendulum is moved. We are supposed to find the change in the period of oscillation under this given condition.
Let us consider the first option,

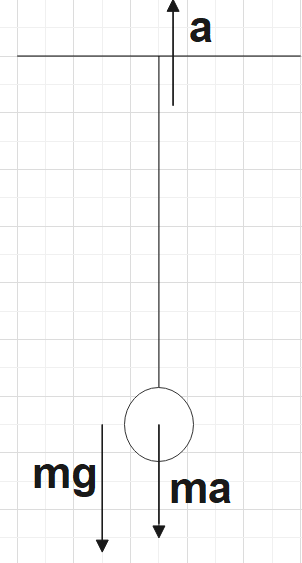
Here since the point of suspension moves upwards, the pseudo force would be downwards. So, the net force would be given by,
${{F}_{net}}=m{{g}_{eff}}=mg+ma$
$\Rightarrow {{g}_{eff}}=a+g$
Now we have the time period of oscillation given by,
$T=2\pi \sqrt{\dfrac{l}{{{g}_{eff}}}}$
That is,
$T\propto \dfrac{1}{\sqrt{{{g}_{eff}}}}$……………………………….. (1)
Since ${{g}_{eff}}\rangle g$, we could say that the time period of oscillation decreases in this case. Hence, option A is true.
For the second option,

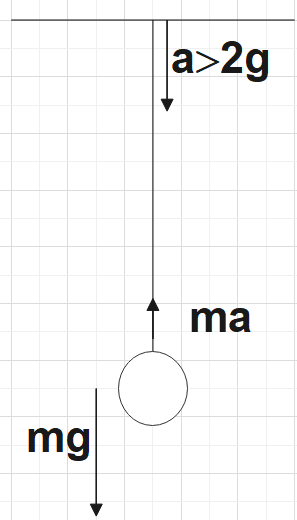
Here the net force could be given as,
${{F}_{net}}=m{{g}_{eff}}=ma-mg$
$\Rightarrow {{g}_{eff}}=a-g$
Since $a\rangle 2g$, which would further imply that ${{g}_{eff}}\rangle g$and from (1) we could conclude that the time period of oscillation would decrease here also. Hence, option B is true.
For the third case,

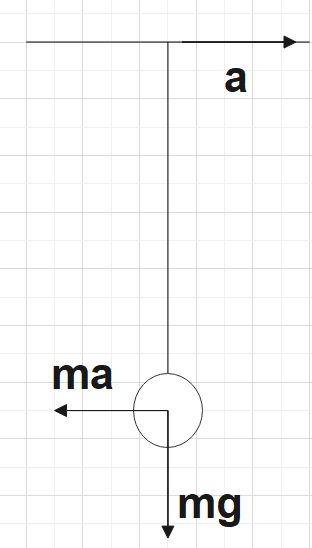
Here the net force would be,
${{F}_{net}}=m{{g}_{eff}}=\sqrt{{{\left( mg \right)}^{2}}+{{\left( ma \right)}^{2}}}$
$\Rightarrow {{g}_{eff}}=\sqrt{{{a}^{2}}+{{g}^{2}}}$
Clearly,${{g}_{eff}}\rangle g$, so here also the time period of oscillation would decrease. Hence option C is false.
Therefore, we found the options A and B to be true.

Note: One should always keep in mind that the direction of the pseudo force would always be in the direction opposite to the direction of the body’s acceleration. For the third case we have simply found the resultant force using vector addition. The key point for the whole solution is that time period decreases with increase in ${{g}_{eff}}$.