Question

Please help How do I graph the polar equation ${{r}^{2}}=4\sin \theta $ ?

Answer 1

Hint: We will first convert the following equation in polar coordinate equation format and solve it accordingly and plot it in graph.

Complete step by step answer:
First we will consider a function of the type:
\[r=f\left( \theta \right)\]
So we will give values of the angle $\theta $ and the function gives you values of $r$.
To graph polar functions, we have to find points that lie at a distance $r$ from the origin and form (the segment $r$) an angle $\theta $ with the x-axis.
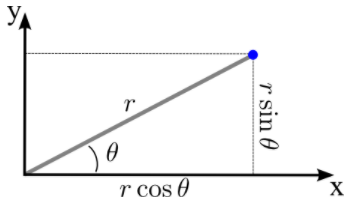
We can calculate Cartesian coordinates of a point with polar coordinates \[(r,\theta )\] by forming the right triangle. The hypotenuse is the line segment from the origin to the point, and its length is \[r\]. The projection of this line segment on the x-axis is the leg of the triangle adjacent to the angle \[\theta \], so \[x=rcos\theta \]. The y-component is determined by the other leg, so \[x=rcos\theta \] .
Our conversion formula is:
$\begin{align}
  & x=r\cos \theta \\
 & y=r\sin \theta \\
\end{align}$

So now coming to our question, we have:
${{r}^{2}}=4\sin \theta $
 Now here we will shift the root on the right hand side, we get:
$r=2\sqrt{\sin \theta }$
Now from this we can see that radius is having a negative number, as such the square of the radius cannot equal a negative number, therefore we must add the following restriction:
\[{{r}^{2}}=4sin(\theta );0\le \theta \le \pi \]
With this, this allows us to take the square root of both sides of the equation without being concerned with the negative values.
So we get:
\[r=2\sqrt{\sin \left( \theta \right)};0\le \theta \le \pi \]
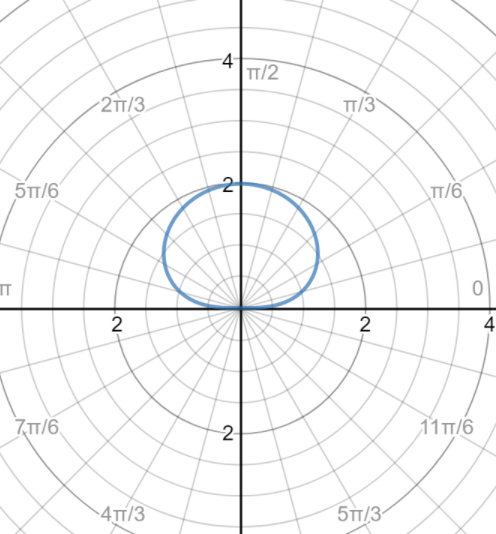
With this we will get a graph of equation as follows:

Note:
A polar equation is any equation that describes a relation between \[r\] and $\theta $, where \[r\] represents the distance from the pole (origin) to a point on a curve, and $\theta $ represents the counterclockwise angle made by a point on a curve, the pole, and the positive x-axis.