Question

Photoelectric effect experiments are performed using three different metal plates p, q and r having work function ${{\phi }_{P}}=2eV$, ${{\phi }_{q}}=2.5eV$ and ${{\phi }_{r}}=3eV$ respectively. A light beam containing wavelengths of 550nm, 450nm, and 350nm with equal intensities illuminates each of the plates. The correct I – V graph for the experiment is:
(Take hc = 1240 eVnm)
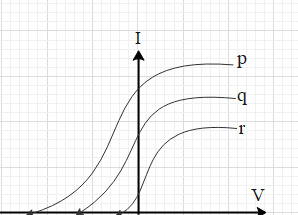
A.

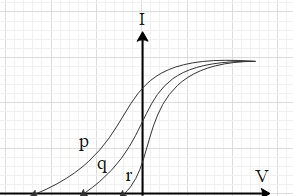
B.

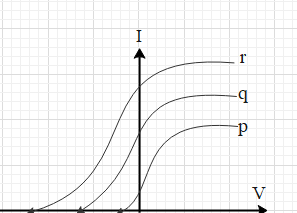
C.

D.

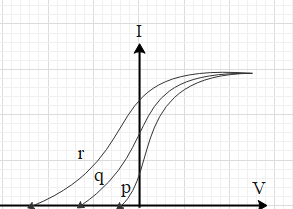
Answer 1

Hint: Saturation current depends on the intensity of light. The more the intensity of the light, the greater will be the value of saturation current. Then find the relation between the stopping voltages of all the three metal plates by using the formula for the stopping voltage.
Formula used:
${{K}_{\max }}=\dfrac{hc}{\lambda }-\phi $
${{V}_{0}}=\dfrac{{{K}_{\max }}}{e}$

Complete step-by-step answer:
When the light of a suitable wavelength falls on a metal plate, if the energy of the photons is greater than the work function of the metal then electrons are ejected out of the metal. If a potential difference with correct polarity is created across these ejected electrons, then there is current in the current. As we increase the potential difference, the current in the circuit increases, and after some value of the potential difference the current saturates (meaning it becomes constant). The value of the saturation current depends on the intensities of the light. The more the intensity of the light, the greater will be the value of saturation current.
In this case, it is given that the intensities of the lights are the same. Therefore, the saturated current in all three circuits will be the same.
Let us now understand what stopping voltage is. Stopping voltage is the minimum reverse potential difference that is needed to produce a zero current in the circuit.
The stopping voltage is equal to the maximum kinetic energy of the electrons per unit charge. And the maximum kinetic energy is given as ${{K}_{\max }}=\dfrac{hc}{\lambda }-\phi $, where h is the Planck’s constant, c is the speed of light in vacuum, $\lambda $is the wavelength of the light and $\phi $ is the work function of the metal.
This means that ${{V}_{0}}=\dfrac{{{K}_{\max }}}{e}=\dfrac{1}{e}\left( \dfrac{hc}{\lambda }-\phi \right)$ ….. (i),
where ‘e’ is the charge on one electron and ${{V}_{0}}$ is the stopping voltage.
Let us calculate the stopping voltages for each of the metal plates.
Substitute the corresponding given values in (i).
$\Rightarrow {{V}_{0,p}}=\dfrac{1}{e}\left( \dfrac{1240}{550}-2 \right)=\dfrac{0.254}{e}$
$\Rightarrow {{V}_{0,q}}=\dfrac{1}{e}\left( \dfrac{1240}{450}-2.5 \right)=\dfrac{0.256}{e}$
$\Rightarrow {{V}_{0,r}}=\dfrac{1}{e}\left( \dfrac{1240}{350}-3 \right)=\dfrac{0.543}{e}$.
Therefore, ${{V}_{0,p}}$<${{V}_{0,q}}$<${{V}_{0,r}}$
The graph, which correctly depicts the concluded data, is in option D. Hence, the correct option is D.

Note: Always remember that the maximum number of electrons available for the conduction of current is equal to the number of photons that falls on the metal plate. Each photon of the light collides with the electron of the metal plate and ejects it out.
The number of photons is directly proportional to the intensity of the light.
Therefore, the saturation current only depends on the intensity of the light. It is independent of the frequency and wavelength of the light.