Question

PART A) A compound is formed by two elements M and N.The element N forms ccp and atoms of M occupy $\text{ }\dfrac{1}{3}\text{ }$of the tetrahedral voids.What is the formula of compound.
PART B ) What kind of defect is shown by $\text{ ZnS }$,$\text{ AgBr }$.

Answer 1

Hint: PART A) Voids are the vacant spaces between the atoms in closed structures. In a 3-D structure, the tetrahedral voids are equal to twice the number of the atoms in the structure. The octahedral voids are equal to the total number of atoms in the structure. The relation can be stated as,
$\begin{align}
  & \text{ Tetrahedral voids = 2 }\times \text{ Octahedral voids } \\
 & \text{ Octahedral voids = Number of atoms in structure } \\
\end{align}$
The ccp structure is analogous to the FCC structure where 8 atoms are at 8 corners and 6 atoms are at each face of the cubic structure.
PART B) The ideal crystal is one which is free from any type of imperfections or defect.The crystal may have the point defect , line defect or etc.The point defect arises due to the displacement of the removal of ions from their own lattice point in the crystal.These are:
1) Schottky defect
2) Frenkel defect

Complete answer:
PART A) Voids are the empty spaces between the particles. In solid state chemistry, the void is referred to as the empty spaces or vacant spaces between the atoms in a closed packed structure. In 3-dimensional close packing results in the two different types of voids. These are:
1) Tetrahedral voids and
2) Octahedral voids
In a cubic close packed structure, the layers are arranged in such a manner that the atom is placed on the triangular void and results in the tetrahedral void. Such a type of void is observed in ABAB …type structure. In the ccp structure, the number of tetrahedral voids is two times that of the number of an atom in a structure. For ‘n’ number of atoms, the tetrahedral voids would be $\text{ 2n }$ .
The octahedral voids are adjacent to tetrahedral voids. These voids are closed by the six neighbouring atoms and thus have the shape of an octahedron. The ccp structure with ‘n’ number of atoms has an ‘n’ number of octahedral voids.
Here, we have given that two elements M and N are forming a compound. Let’s the compound be $\text{ }{{\text{M}}_{\text{x}}}{{\text{N}}_{\text{y}}}\text{ }$ . we are interested to find the value of x and y.
The N element forms a cubic close packing structure. The cubic close packing structure has the 8 atoms at the 8 corners of the structure and 6 atoms at the centre of the face. The total number of atom the ccp is equal to,
$\text{ No}\text{.of atom in ccp = }\dfrac{1}{8}\times \text{8 atoms at corner + }\dfrac{1}{2}\times 6\text{ atoms at face = 1 + 3 =4 }$
Thus, the ccp structure has 4 atoms per unit cell.
The octahedral and tetrahedral voids are related as,
$\text{ Tetrahedral voids = 2 }\times \text{ Octahedral voids }$
Here, the M occupies the $\text{ }\dfrac{1}{3}\text{ }$ of the tetrahedral void. These are given as,
$\begin{align}
  & \text{ M = }\dfrac{1}{3}\times \text{2 }\times \text{ number of atoms } \\
 & \Rightarrow \text{ = }\dfrac{1}{3}\times \text{2 }\times \text{ 4} \\
 & \therefore \text{M = }\dfrac{8}{3}\text{ } \\
\end{align}$
Thus the formula for the compound is,
$\begin{align}
  & \text{M : N }\Rightarrow \dfrac{8}{3}\text{ : 4 } \\
 & \therefore \text{M : N }=\text{ 8 : 12 or 2 : 3 } \\
\end{align}$
So, the 2 atoms of M and 3 of the N combine to form a $\text{ }{{\text{M}}_{\text{2}}}{{\text{N}}_{\text{3}}}\text{ }$ compound. Here, $\text{ x = 2 , y = 3 }$
Hence, the compound is $\text{ }{{\text{M}}_{\text{2}}}{{\text{N}}_{\text{3}}}\text{ }$.
PART B) The defect which arises when the ion occupies an interstitial position in the lattice structure is called the frenkel defect.
In $\text{ AgBr }$ structure , the one of the$\text{ A}{{\text{g}}^{\text{+}}}\text{ }$ occupies the the interstitial position rather than its site in the lattice.A vacancy is a shown in the figure.

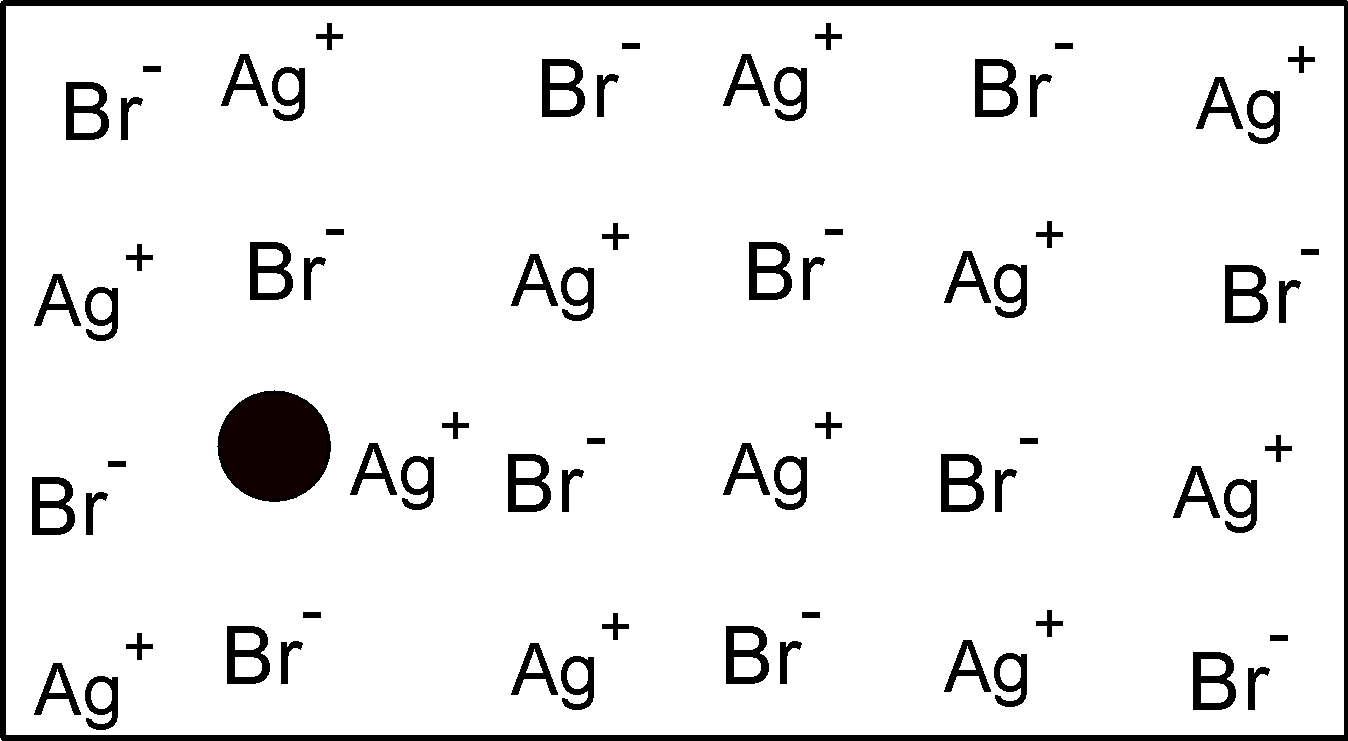
$\text{ ZnS }$ is another crystal which shows the frenkel defect .$\text{ Z}{{\text{n}}^{\text{2+}}}\text{ }$ ions are entrapped in the interstitial space leaving vacancies in the lattice.

Note:
Note that, the total number of voids present in the ccp structure at different location .thus can be calculated as:
For ccp,
No. of atoms is 4, so octahedral voids are equal to 4 and tetrahedral voids are two times the octahedral voids. Thus the total number of voids per unit cell in ccp is equal to, $\text{ }{{\left( \text{No}\text{.of voids per unit cell} \right)}_{\text{ccp}}}\text{ = 8 + 4 = 12 }$
For hcp, the total number of voids are,$\text{ }{{\left( \text{No}\text{.of voids per unit cell} \right)}_{\text{hcp}}}\text{ = 12 + 6 = 18 }$