
P \[\left( -1,4 \right)\], Q \[\left( 11,-8 \right)\] divides AB harmonically in the ratio \[3:2\] then A,B are?
Answer
539.4k+ views
Hint:Using the section formula method we first multiply the \[x\] coordinates with the ratio \[3:2\] and then do the same for \[y\] coordinates as well.
For \[x\] coordinates and coordinates of A and B as \[\left( a,b \right)\] and \[\left( x,y \right)\] with ratio
\[\left( m:n \right)\]:
\[\dfrac{mx+na}{m+n}\]
For \[y\] coordinates and coordinates of A and B as \[\left( a,b \right)\] and \[\left( x,y \right)\] with ratio\[\left( m:n \right)\]:
\[\dfrac{my+nb}{m+n}\]
The previous formula was applied for P coordinate and now we will do the same for Q coordinates as well. The ratio of \[3:2\] will change to \[-3:2\] as Q is a harmonic conjugate of P.
Complete step by step solution:
Now as given in the question, we first form a coordinate diagram where P is the midpoint with A, B as extreme and the distance of AP is 3 and the distance of PB is 2.
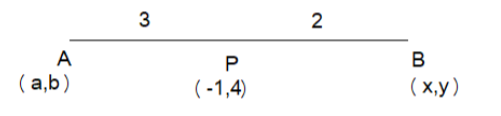
After this let us form an equation with the help of A's coordinate and B's coordinate with midpoint as
\[\left( -1,4 \right)\].
The equation for the \[a\] or \[x\] coordinate is given as:
\[\Rightarrow \dfrac{3\times x+2\times a}{3+2}=-1\]
\[\Rightarrow 3x+2a=-5\] …(1)
The equation for the \[b\] or \[y\] coordinate is given as:
\[\Rightarrow \dfrac{3\times y+2\times b}{3+2}=4\]
\[\Rightarrow 3y+2b=20\] …(2)
We now find equation for \[x\] and \[y\] with midpoint being \[\left( 11,-8 \right)\] and the ratio of distance from AQ to QB as \[\left( -3:2 \right)\] as Q is harmonic conjugate of P.
The equation for the \[a\] or \[x\] coordinate is given as:
\[\Rightarrow \dfrac{-3\times x+2\times a}{-3+2}=11\]
\[\Rightarrow -3x+2a=-11\] …(3)
The equation for the \[b\] or \[y\] coordinate is given as:
\[\Rightarrow \dfrac{-3\times y+2\times b}{-3+2}=8\]
\[\Rightarrow -3y+2b=8\] …(4)
Now we equate the Equation 1, 2, 3 and 4; So as to find the value of a, b. First we find for the value of a by equating equation 1,3.
\[\begin{align}
& \text{ }3x+2a=-5 \\
& -3x+2a=-11 \\
& \text{ +}4a=-16 \\
\end{align}\]
\[\Rightarrow a=-4\]
We get the value of \[a\] as \[-4\] and to find the value of \[x\] we place the value of \[a\] in \[3x+2a= -5\].
\[\Rightarrow 3x+2\times -4=-5\]
\[\Rightarrow 3x=8-5\]
\[\Rightarrow x=1\]
Then we find for the value of b by Equating equation 2,4.
\[\begin{align}
& \text{ }3y+2b=20 \\
& -3y+2b=8 \\
& \text{ +}4b=28 \\
\end{align}\]
\[\Rightarrow b=7\]
We get the value of \[b\] as \[7\] and to find the value of \[x\] we place the value of \[b\] in \[-3y+2b=8\].
\[\Rightarrow -3y+2\times 7=8\]
\[\Rightarrow -3y=-14+8\]
\[\Rightarrow y=2\]
Therefore, the value of a, b or A, B is given as \[\left( -4:7 \right)\]
Note: The term harmonic conjugate means that if the line is divided let say in ratio of \[\text{AC:BC = AD:BD}\] we can say that C and D are cutting the line AB harmonically and that AB and CD are harmonic conjugates.

For \[x\] coordinates and coordinates of A and B as \[\left( a,b \right)\] and \[\left( x,y \right)\] with ratio
\[\left( m:n \right)\]:
\[\dfrac{mx+na}{m+n}\]
For \[y\] coordinates and coordinates of A and B as \[\left( a,b \right)\] and \[\left( x,y \right)\] with ratio\[\left( m:n \right)\]:
\[\dfrac{my+nb}{m+n}\]
The previous formula was applied for P coordinate and now we will do the same for Q coordinates as well. The ratio of \[3:2\] will change to \[-3:2\] as Q is a harmonic conjugate of P.
Complete step by step solution:
Now as given in the question, we first form a coordinate diagram where P is the midpoint with A, B as extreme and the distance of AP is 3 and the distance of PB is 2.
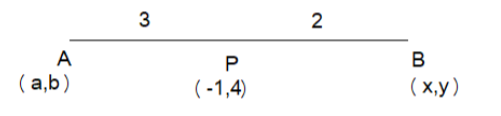
After this let us form an equation with the help of A's coordinate and B's coordinate with midpoint as
\[\left( -1,4 \right)\].
The equation for the \[a\] or \[x\] coordinate is given as:
\[\Rightarrow \dfrac{3\times x+2\times a}{3+2}=-1\]
\[\Rightarrow 3x+2a=-5\] …(1)
The equation for the \[b\] or \[y\] coordinate is given as:
\[\Rightarrow \dfrac{3\times y+2\times b}{3+2}=4\]
\[\Rightarrow 3y+2b=20\] …(2)
We now find equation for \[x\] and \[y\] with midpoint being \[\left( 11,-8 \right)\] and the ratio of distance from AQ to QB as \[\left( -3:2 \right)\] as Q is harmonic conjugate of P.
The equation for the \[a\] or \[x\] coordinate is given as:
\[\Rightarrow \dfrac{-3\times x+2\times a}{-3+2}=11\]
\[\Rightarrow -3x+2a=-11\] …(3)
The equation for the \[b\] or \[y\] coordinate is given as:
\[\Rightarrow \dfrac{-3\times y+2\times b}{-3+2}=8\]
\[\Rightarrow -3y+2b=8\] …(4)
Now we equate the Equation 1, 2, 3 and 4; So as to find the value of a, b. First we find for the value of a by equating equation 1,3.
\[\begin{align}
& \text{ }3x+2a=-5 \\
& -3x+2a=-11 \\
& \text{ +}4a=-16 \\
\end{align}\]
\[\Rightarrow a=-4\]
We get the value of \[a\] as \[-4\] and to find the value of \[x\] we place the value of \[a\] in \[3x+2a= -5\].
\[\Rightarrow 3x+2\times -4=-5\]
\[\Rightarrow 3x=8-5\]
\[\Rightarrow x=1\]
Then we find for the value of b by Equating equation 2,4.
\[\begin{align}
& \text{ }3y+2b=20 \\
& -3y+2b=8 \\
& \text{ +}4b=28 \\
\end{align}\]
\[\Rightarrow b=7\]
We get the value of \[b\] as \[7\] and to find the value of \[x\] we place the value of \[b\] in \[-3y+2b=8\].
\[\Rightarrow -3y+2\times 7=8\]
\[\Rightarrow -3y=-14+8\]
\[\Rightarrow y=2\]
Therefore, the value of a, b or A, B is given as \[\left( -4:7 \right)\]
Note: The term harmonic conjugate means that if the line is divided let say in ratio of \[\text{AC:BC = AD:BD}\] we can say that C and D are cutting the line AB harmonically and that AB and CD are harmonic conjugates.

Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




