Question

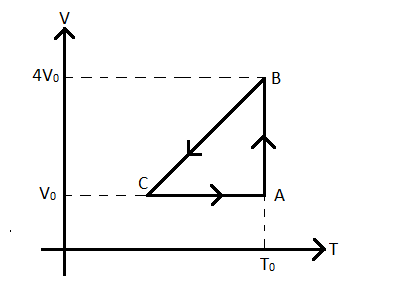
One mole of an ideal gas at initial state $A$ undergoes a cyclic process $ABCA$, as shown in fig. Its pressure at $A$ is ${{P}_{0}}$. Choose the correct options from the following

This question has multiple correct options.
A) Internal energies at $A$ and $B$ are same
B) Work done by the gas in the process $AB$ is ${{P}_{0}}{{V}_{0}}\ln 4$
C) Pressure at $C$ is $\dfrac{{{P}_{0}}}{4}$
D) Temperature at $C$ is $\dfrac{{{T}_{0}}}{4}$

Answer 1

Hint: This problem can be solved by the thorough understanding of the first law of thermodynamics and the ideal gas equation. The equation for the work done in an isothermal process will also be useful to find out the work done in the process $AB$.

Formula used:
$PV=nRT$
${{W}_{isothermal}}=nRT\ln \left( \dfrac{{{V}_{f}}}{{{V}_{i}}} \right)$

Complete step by step answer:
Let us analyze the options one by one.
Option A) Checking the internal energies at $A$ and $B$.
Now, the internal energy of a gas depends solely upon its temperature. Since the temperature of the ideal gas at the points $A$ and $B$ are the same and equal to ${{T}_{0}}$, the internal energies of the gas at $A$ and $B$ are also the same.
Therefore, option $A)$ is correct.
Option B) Let us find out the work done by the gas in the process $AB$.
In the process $AB$, as we can see from the figure, the temperature of the gas remains constant and equal to ${{T}_{0}}$. Hence, the process is an isothermal process.
Now, for an isothermal process, the work ${{W}_{isothermal}}$ done by a gas at a constant temperature $T$ is given by
${{W}_{isothermal}}=nRT\ln \left( \dfrac{{{V}_{f}}}{{{V}_{i}}} \right)$ --(1)
Where $n$ is the number of moles of the gas, $R=8.314J.mo{{l}^{-1}}{{K}^{-1}}$ is the universal gas constant and ${{V}_{f}},{{V}_{i}}$ are the final and initial volumes of the gas respectively.
Now, according to the question, the number of moles given to us is one.
$\therefore n=1$
Also, $T={{T}_{0}}$.
Now, according to the ideal gas equation the pressure $P$, volume $V$, number of moles $n$ and temperature $T$ of a gas are related as
$PV=nRT$ --(2)
From (2), we get
${{P}_{A}}{{V}_{A}}=1R{{T}_{0}}$ --(3)
Where ${{P}_{A}},{{V}_{A}},{{T}_{0}}$ are the pressure, volume and temperature of the gas at $A$.
According to the question and the figure
${{P}_{A}}={{P}_{0}}$ --(4)
${{V}_{A}}={{V}_{0}}$ --(5)
Now, using (1), we get the work done $W$ by the gas in the process $AB$ as
$W=1R{{T}_{0}}\ln \left( \dfrac{{{V}_{B}}}{{{V}_{A}}} \right)$ -(6)
Where ${{V}_{B}}=4{{V}_{0}}$ is the volume at $B$.
Putting (3), (4), (5) in (6), we get
$W={{P}_{0}}{{V}_{0}}\ln \left( \dfrac{4{{V}_{0}}}{{{V}_{0}}} \right)={{P}_{0}}{{V}_{0}}\ln \left( 4 \right)$
Therefore, option B) is correct.
Option C and D) Now we cannot find the pressure and temperature of $C$ as there will be more unknowns (temperature and pressure) than equations while solving. Two out of three among the pressure, volume and temperature had to be known to get the value of the third one. However, that is not the case and hence, we cannot verify whether options C) and D) are correct or not.
Therefore, the only correct options are A) and B).

Note:
Students must note that the plot given is in fact a volume-temperature plot of a thermodynamic process of an ideal gas. In most cases, conventionally, a pressure volume plot is provided for any process of a gas and that notion gets stuck in the mind of the students and they might proceed in the same way in this problem also. However, they must realize this fact and therefore, before solving such graphical questions, always analyze what physical quantities are given along the axes and represented by the plot.