Question

On lighting a rocket cracker it gets projected in a parabolic path and reaches a maximum height of $4m$ when it is 6m away from the point of projection. Finally it reaches the ground 12m away from the starting point. Find the angle of projection.

Answer 1

Hint: In this particular question use the common fact that the rocket is always going upwards. And it is given it follows a parabolic path so the parabola should be vertically downwards so assume the equation of the parabola, ${x^2} = - 4ay$, so use these concepts to reach the solution of the question.

Complete step-by-step answer:
The pictorial representation of the given problem is shown below

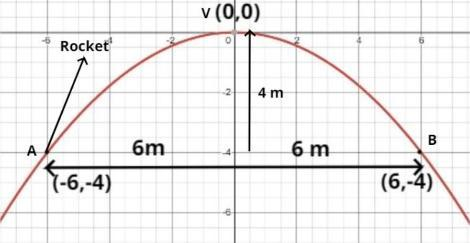
It is a common fact that the rocket is always going upwards.
And it is given it follows a parabolic path so the parabola should be vertically downwards.
So, let the equation of parabola
${x^2} = - 4ay..............\left( 1 \right)$
It is given that it reaches a maximum height 4m when it is 6m away from the starting point.
$\therefore $It is passing from$\left( { - 6, - 4} \right)$, so this point satisfies the equation of parabola.
From equation 1
$
  {\left( { - 6} \right)^2} = - 4a\left( { - 4} \right) \Rightarrow 36 = 16a \Rightarrow a = \dfrac{9}{4} \\
   \Rightarrow {x^2} = - 4\left( {\dfrac{9}{4}} \right)y = - 9y................\left( 2 \right) \\
$
Now we have to find out the angle of projection of the rocket.
So, we know angle of projection is the slope of the parabola at point $\left( { - 6, - 4} \right)$
Therefore slope${\text{ = }}\dfrac{{dy}}{{dx}} = \tan \theta $
From equation 2
\[y = \dfrac{{ - {x^2}}}{9}\]
Therefore differentiate the equation of parabola w.r.t.$x$
\[
  \dfrac{{dy}}{{dx}} = \dfrac{{ - 1}}{9}\left( {2x} \right) \\
  \dfrac{{dy}}{{dx}}{\text{ at point }}\left( { - 6, - 4} \right) = \dfrac{{ - 1\left( {2 \times \left( { - 6} \right)} \right)}}{9} = \dfrac{{12}}{9} = \dfrac{4}{3} \\
   \Rightarrow \tan \theta = \dfrac{4}{3} \Rightarrow \theta = {\tan ^{ - 1}}\left( {\dfrac{4}{3}} \right) \\
\]
So this is the required angle of projection.

Note: Whenever we face such type of problem the key point we have to remember is that the rocket is always goes up so the parabola is opening vertically downwards, then according to given conditions mark all the points and satisfy any point in the equation of parabola except (0, 0), so we get the value of $a$, then differentiate the equation of parabola and satisfying the starting points, then we will get the required angle of projection.