Question

Obtain an expression for intensity of electric field at a point in end on position i.e. axial position of an electric dipole

Answer 1

Hint: In this question we have been asked to obtain an expression for intensity of electric field at a point in end on position. Therefore, we shall use the formula for intensity of electric fields to obtain the required answer. We know that electric field intensity is the force experienced by a positive charge at a certain point in space.

Complete step by step solution:
Let \[q,-q\] be the point charge separated by distance 2a as shown in the figure. The line OP is the axial line of electric dipole.
                  

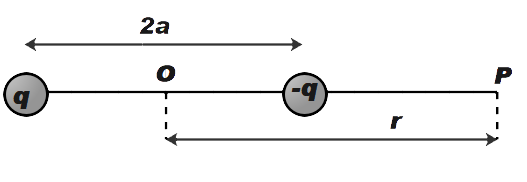
Therefore, to calculate the electric field at the end point of dipole i.e. point P.
Let \[{{E}_{1}}\] and \[{{E}_{2}}\] be the electric field on point P due to charge \[q,-q\] respectively.
Therefore, we can say that,
\[{{E}_{1}}=\dfrac{kq}{{{\left( r-a \right)}^{2}}}\] …………………. (1)
Similarly,
\[{{E}_{2}}=\dfrac{kq}{{{\left( r+a \right)}^{2}}}\] …………………. (2)
Now, the intensity of electric field at point P will be given by,
\[E={{E}_{1}}-{{E}_{2}}\] ………………………. (3)
Therefore, from (1), (2) and (3)
We get,
\[E=\dfrac{kq}{{{\left( r-a \right)}^{2}}}-\dfrac{kq}{{{\left( r+a \right)}^{2}}}\]
On solving above equation,
We get,
\[E=\dfrac{kq\times 4ra}{{{\left( {{r}^{2}}-{{a}^{2}} \right)}^{2}}}\] ……………….. (4)
Now, we know that the dipole for a charge is given by,
\[p=q\times 2a\]
After substituting the above value in equation (4)
We get,
\[E=\dfrac{k\times 2pr}{{{\left( {{r}^{2}}-{{a}^{2}} \right)}^{2}}}\]
Now, if we assume that, \[r\gg a\], then the above equation can be written as,
\[E=k\dfrac{2pr}{{{r}^{4}}}\]
Therefore,
\[E=k\dfrac{2p}{{{r}^{3}}}\]
The vector form of the above equation is,
\[\overrightarrow{E}=k\dfrac{2\overrightarrow{p}}{{{r}^{3}}}\]
Where,
\[k=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\]

Note: The intensity of the electric field at any point is the measure of the force that is experienced by the charge. The unit of electric field intensity is volts per metre. The electric field intensity is a vector quantity. The direction of the electric field is usually the direction of force experienced by a unit positive charge.