Question

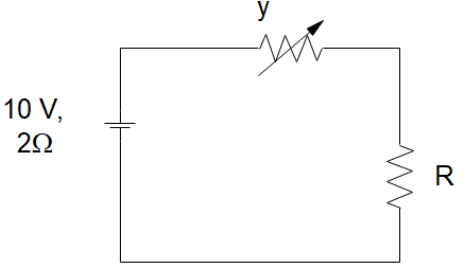
In the figure shown the power generated in Y is maximum when $ y = 5\Omega $ . Then R is

A) 2Ω
B) 6Ω
C) 5Ω
D) 3Ω

Answer 1

Hint: In this solution, we will use the formula of power generated in Y and its dependence on current and resistance to determine the value of resistance for which the power will be maximum. To find the value of the variable resistance, we will differentiate the equation of power with respect to the fixed resistance.

Formula used: In this solution, we will use the following formula:
- Power dissipated in a resistance $ P = {i^2}R $ where $ i $ is the current in the circuit and $ R $ is the value of the resistance
- Ohm’s law: $ V = iR $ where $ V $ is the voltage

Complete step by step answer:
In the diagram given to us, we can see that the two resistances are in series. So, the net resistance of the circuit will be
 $ {R_{net}} = 2 + y + R $
Then the current in the circuit will be
 $ i = \dfrac{V}{R} = \dfrac{V}{{2 + y + R}} $
The power dissipated in the variable resistor would be
 $ P = {i^2}y $
Which can be written as
 $ P = {\left( {\dfrac{V}{{2 + y + R}}} \right)^2}y $
Then the maximum power will be dissipated when $ dP/dy = 0 $ . So differentiating the above equation with respect to $ y $ , we get
 $ \dfrac{{dP}}{{dy}} = \dfrac{{{{(2 + y + R)}^2}(1) - y(2)(2 + R + y)}}{{{{(2 + R + y)}^4}}} = 0 $
Then cross multiplying the denominator, we can write
 $ {(2 + y + R)^2}(1) - y(2)(2 + R + y) = 0 $
Since $ y = 5\Omega $ , we can solve the above equation of $ R $ as
 $ R = 3\Omega $
Hence the correct choice will be option (D).

Note:
It is easy to get confused that if the variable resistor already has a fixed value, we cannot differentiate the equation of power dissipated in it. However, the value of the variable resistor is fixed such that the power dissipated is maximum and since that depends on both the variable resistor and the fixed resistor, we should substitute the value only after differentiating the power dissipated in the resistor.