Questions & Answers
Question
AnswersWhat note on a typical biogas plant. How microbes help in the production of biogas.
Answer
Verified128.4k+ views
Hint: A biogas plant is a plant that treats the wastes. Biogas is the mixture of gases that are produced by the breakdown of organic matter within the absence of oxygen. In India, it is called ‘Gobar gas’.
Complete answer:
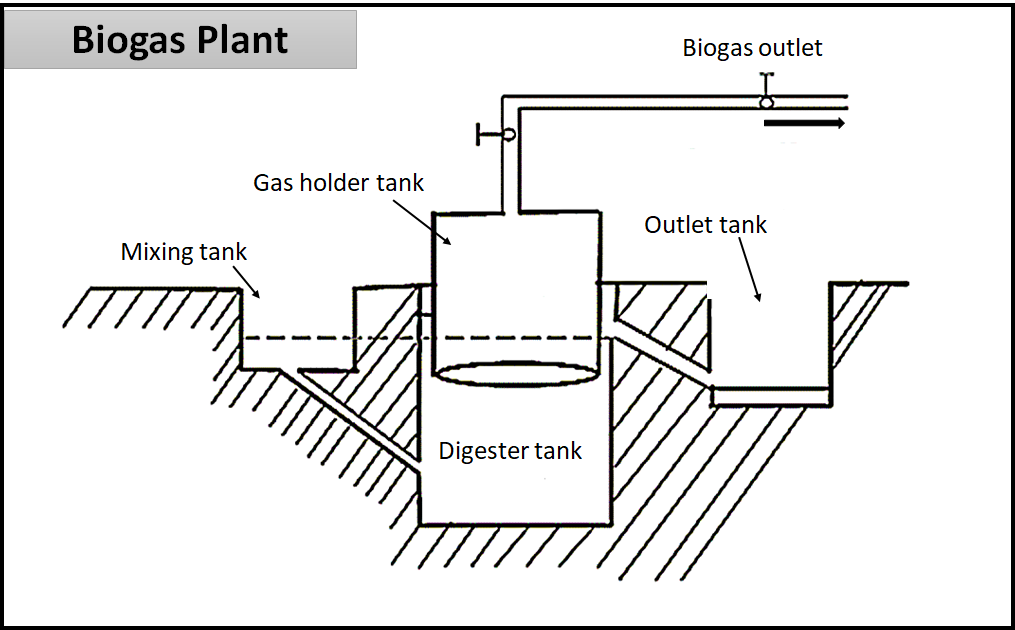
A biogas plant is a name frequently given to an anaerobic digester that treats farm wastes or energy crops. It is produced using anaerobic digesters, air-tight tanks with different configurations. These plants are often fed with energy crops like maize silage or biodegradable wastes including sewage sludge and food waste. During the method, the micro-organisms transform biomass waste into biogas (mainly methane and carbon dioxide).
Biogas Plant:
-The biogas plant consists of a source to provide the feedstock, a digestion tank for biogas production, a biogas recovery unit to isolate the produced biogas, and a warmth exchanger to take care of the temperature of the digester.
-The biowaste and the slurry of dung are fed into an anaerobic digester.
-The slurry is roofed with a floating cover. The gas produced because of microbial activity makes the quilt rise upwards.
-The produced biogas is supplied to the respective places through connected pipes and may be used for cooking and lighting.
-The used slurry is removed through an outlet and might be used as fertilizer later.
Biogas is the combination of gases created by the microorganisms. Methane is the main gas present within the biogas mixture. Certain bacteria grow under anaerobic conditions and produce a large amount of methane alongside carbon dioxide and hydrogen. The bacteria (Methanobacterium) which produce the gaseous mixture are collectively referred to as methanogens.
Methanobacterium exists inside the rumen of the cattle and the sludge generated during sewage treatment. The Methanobacterium digests the cellulose present within the food of the cattle. The dung then produced by the cattle contains these methanogens which are used for the construction of biogas.
Note: The biogas produced is often used for lighting and cooking purposes. Biogas is often compressed after the removal of carbon dioxide to power automobiles. Biogas is estimated to possess the potential to exchange around 17% of auto fuel. Biogas is taken into account to be a renewable resource.
Complete answer:
A biogas plant is a name frequently given to an anaerobic digester that treats farm wastes or energy crops. It is produced using anaerobic digesters, air-tight tanks with different configurations. These plants are often fed with energy crops like maize silage or biodegradable wastes including sewage sludge and food waste. During the method, the micro-organisms transform biomass waste into biogas (mainly methane and carbon dioxide).
Biogas Plant:
-The biogas plant consists of a source to provide the feedstock, a digestion tank for biogas production, a biogas recovery unit to isolate the produced biogas, and a warmth exchanger to take care of the temperature of the digester.
-The biowaste and the slurry of dung are fed into an anaerobic digester.
-The slurry is roofed with a floating cover. The gas produced because of microbial activity makes the quilt rise upwards.
-The produced biogas is supplied to the respective places through connected pipes and may be used for cooking and lighting.
-The used slurry is removed through an outlet and might be used as fertilizer later.
Biogas is the combination of gases created by the microorganisms. Methane is the main gas present within the biogas mixture. Certain bacteria grow under anaerobic conditions and produce a large amount of methane alongside carbon dioxide and hydrogen. The bacteria (Methanobacterium) which produce the gaseous mixture are collectively referred to as methanogens.
Methanobacterium exists inside the rumen of the cattle and the sludge generated during sewage treatment. The Methanobacterium digests the cellulose present within the food of the cattle. The dung then produced by the cattle contains these methanogens which are used for the construction of biogas.
Note: The biogas produced is often used for lighting and cooking purposes. Biogas is often compressed after the removal of carbon dioxide to power automobiles. Biogas is estimated to possess the potential to exchange around 17% of auto fuel. Biogas is taken into account to be a renewable resource.