Question

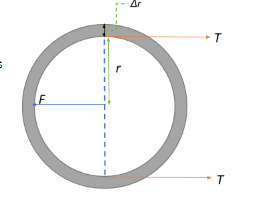
Maximum excess pressure inside a thin-walled steel tube of radius $r$ and thickness $\Delta r \left(<< r\right)$, so that the tube would not rupture would be (breaking stress of steel =

A.$\sigma_{max}$)
B.$\sigma_{max} \times \dfrac{r}{\Delta r}$
C.$\sigma_{max} \times \dfrac{\Delta r}{r}$
D.$\sigma_{max}$
E.$\sigma_{max} \times \dfrac{2\Delta r}{r}$

Answer 1

Hint: At equilibrium the force exerted from the inside is balanced out by the tension experienced by the walls of the tube. Therefore, find the expressions for the previously mentioned forces and equate them to obtain an expression for the maximum internal pressure. Also remember to account for all tension points as a result of the applied force.

Complete answer:
Let us deconstruct the question and deduce the influencing parameters.
We have a thin walled tube with radius $r \Rightarrow$ diameter $d = 2r$ and thickness $\Delta r$.
Let the length of the tube be $L$.
An internal pressure $P$ causes tension $T$ in the walls of the tube. Therefore, the two forces at play are the force on the walls exerted by the internal pressure and the consequent tension produced in the tube walls,i.e.,
$F_{on\;walls} = P \times A = P \times 2\times r \times L$
The force acting on a point on the wall tries to elongate the tube along the axis of the applied force. This produces regions of stress at points perpendicular to the force direction. This stress produces tension, which is basically the reaction of the tube to the applied force, and is hence directed opposite to the direction of the applied force.
Now, since the stress here is associated with stretching forces, we can call it tensile stress. Thus, from the general equation for tensile stress we have:
Stress $\sigma = \dfrac{F}{A}$ and in this case, since the force acting on the tube walls ($\Delta r$) is tension, it becomes $\sigma = \dfrac{T}{A} \Rightarrow T=\sigma \times A = \sigma \times \Delta r \times L$
We have mentioned above that there will be two regions of stress produced at points perpendicular to force direction. As a consequence, the total tension produced on the tube walls will be $2T$
Now, breaking stress is the maximum stress that the tube can experience beyond which the tube will rupture. At this point, force from internal pressure(which is maximum) perfectly balances out the tension experienced by tube walls:
$F_{on\;walls} = 2T \Rightarrow P_{max} \times 2\times r \times L = 2 \times \sigma_{max} \times \Delta r \times L$
From this state of equilibrium, we can calculate the maximum internal pressure.
$P_{max} = \sigma_{max} \times \dfrac{\Delta r}{r}$
Therefore, the correct option would be B. $\sigma_{max} \times \dfrac{\Delta r}{r}$

Note:
While determining the magnitude of tension experienced as a result of a stretching force in one direction, it is important to remember that for a tube, the point force produces two stress points on the opposite sides of the circumference perpendicular to the direction of the applied force
Also recall that here we are considering only the tangential or circumferential stress since pressure acts inside the tube in all directions and is directed towards the circumference of the tube, and the tension thus produced is tangential.