Question

Let X be any point on the side BC of a triangle ABC. If XM, XN are drawn parallel to BA and CA, BA in M, N respectively: MN meets BC produced in T, prove that TX2=TB x TC.

Answer 1

Hint: In this question it is said that the line XM is parallel to the line AB and the line XN is parallel to the line BA, so we will apply the basic proportionality theorem in the triangle TXM and the triangle TMC and find the ratios of the sides of these triangles and then by further solving we will prove the desired relation as given in the question.

Complete step-by-step answer:
It is being that XM is parallel to BA and XN is parallel to CA so, we can write it as:
\[XM\parallel BA\] and \[XN\parallel CA\]
 

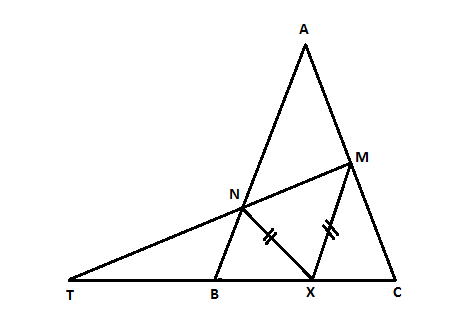
Consider \[\Delta TXM\]here the line \[XM\parallel BN\]since line\[XM\parallel BA\], so by using the basic proportionality theorem we can write
\[\dfrac{{TB}}{{TX}} = \dfrac{{TN}}{{TM}} - - (i)\]
Now we consider the\[\Delta TMC\], here by using the basic proportionality theorem we can write
\[\Rightarrow \dfrac{{TX}}{{TC}} = \dfrac{{TN}}{{TM}} - - (ii)\]
Now from the equations (i) and (ii), we can write
\[\Rightarrow \dfrac{{TB}}{{TX}} = \dfrac{{TX}}{{TC}}\]
Hence by further solving the obtained equation we can say
\[T{X^2} = TB \cdot TC\]
Hence proved that \[T{X^2} = TB \cdot TC\]

Note: Students must note that if a line is drawn parallel to one side of a triangle intersecting the other two sides of a triangle intersecting the other two sides at different points than the other two sides will be divided in the same ratio.