Question

Let $S\left( \alpha \right)=\left\{ \left( x,y \right):{{y}^{2}}\le x,0\le x\le \alpha \right\}$ and $A\left( \alpha \right)$is area of the region $S\left( \alpha \right)$. If for a $\lambda ,0<\lambda <4,A\left( \lambda \right):A\left( 4 \right)=2:5,$ then $\lambda $ equals
A. \[2{{\left( \dfrac{4}{25} \right)}^{\dfrac{1}{3}}}\]
B. \[4{{\left( \dfrac{2}{5} \right)}^{\dfrac{1}{3}}}\]
C. \[4{{\left( \dfrac{4}{25} \right)}^{\dfrac{1}{3}}}\]
D. \[2{{\left( \dfrac{2}{5} \right)}^{\dfrac{1}{3}}}\]

Answer 1

Hint: First we will plot the graph and identify the region for $A\left( \lambda \right)$ then we will write the given parabolic equation in form of x and integrate it from $x=0\text{ to }x=\lambda $, after integrating we will simply apply the final condition given in the question and then obtain the value of $\lambda $.

Complete step by step answer:
Given that, $S\left( \alpha \right)=\left\{ \left( x,y \right):{{y}^{2}}\le x,0\le x\le \alpha \right\}$ and $A\left( \alpha \right)$is area of the region $S\left( \alpha \right)$:

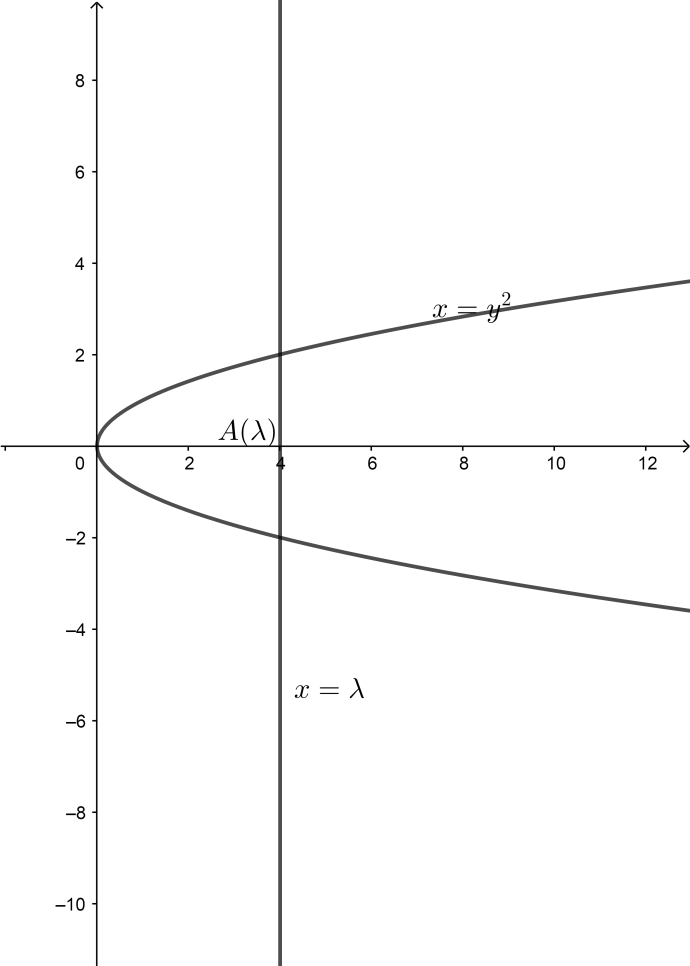
Now, We see that $A\left( \lambda \right)$ is the region bounded by $x={{y}^{2}}$ from $x=0\text{ to }x=\lambda $, so to find $A\left( \lambda \right)$ we will integrate the parabolic equation from $0$ to $\lambda $ :
To start the integration first write the equation in form of x such that: $x={{y}^{2}}\Rightarrow y=\sqrt{x}$
Now we will integrate the following, to integrate it we will use the power rule that is : \[\int{f{{(x)}^{n}}dx=\dfrac{f{{(x)}^{n+1}}}{n+1}}\]
So:
$\begin{align}
  & A\left( \lambda \right)=2\int\limits_{0}^{\lambda }{\sqrt{x}}dx\Rightarrow 2{{\left[ \dfrac{\left( {{x}^{\dfrac{1}{2}+1}} \right)}{\left( \dfrac{1}{2}+1 \right)} \right]}^{\lambda }}_{0} \\
 & \Rightarrow 2{{\left[ \dfrac{\left( {{x}^{\dfrac{3}{2}}} \right)}{\left( \dfrac{3}{2} \right)} \right]}^{\lambda }}_{0} \\
\end{align}$
 Now we will apply the upper limit and the lower limit into the obtained integral we get:
$2{{\left[ \dfrac{\left( {{x}^{\dfrac{3}{2}}} \right)}{\left( \dfrac{3}{2} \right)} \right]}^{\lambda }}_{0}\Rightarrow 2\left[ \dfrac{\left( {{\lambda }^{\dfrac{3}{2}}} \right)}{\left( \dfrac{3}{2} \right)} \right]-2\left[ \dfrac{\left( {{0}^{\dfrac{3}{2}}} \right)}{\left( \dfrac{3}{2} \right)} \right]\Rightarrow \dfrac{4}{3}{{\lambda }^{\dfrac{3}{2}}}$
Therefore , $A\left( \lambda \right)=\dfrac{4}{3}{{\lambda }^{\dfrac{3}{2}}}\text{ }.......\text{Equation 1}\text{.}$
Now it is given in the question that: \[\dfrac{A(\lambda )}{A(4)}=\dfrac{2}{5},(0<\lambda <4)\]
We will put the value of $A\left( \lambda \right)$ from equation 1 into the above mentioned equation:
\[\begin{align}
  & \dfrac{A(\lambda )}{A(4)}=\dfrac{2}{5} \\
 & \Rightarrow \dfrac{\left( \dfrac{4}{3}{{\lambda }^{\dfrac{3}{2}}} \right)}{\left( \dfrac{4}{3}{{4}^{\dfrac{3}{2}}} \right)}=\dfrac{2}{5}\Rightarrow \dfrac{{{\lambda }^{\dfrac{3}{2}}}}{{{4}^{\dfrac{3}{2}}}}=\dfrac{2}{5} \\
\end{align}\]
Now we will square both the sides:
\[\begin{align}
  & \Rightarrow {{\left( \dfrac{{{\lambda }^{\dfrac{3}{2}}}}{{{4}^{\dfrac{3}{2}}}} \right)}^{2}}={{\left( \dfrac{2}{5} \right)}^{2}} \\
 & \Rightarrow {{\left( \dfrac{\lambda }{4} \right)}^{3}}={{\left( \dfrac{2}{5} \right)}^{2}}\Rightarrow {{\left( \dfrac{\lambda }{4} \right)}^{3}}=\left( \dfrac{4}{25} \right) \\
\end{align}\]
Again we will be taking cube roots on both sides:
\[\Rightarrow \left( \dfrac{\lambda }{4} \right)={{\left( \dfrac{4}{25} \right)}^{\dfrac{1}{3}}}\Rightarrow \lambda =4{{\left( \dfrac{4}{25} \right)}^{\dfrac{1}{3}}}\]
Therefore the correct answer is option C.

Note:
Remember that a region bounded from point $a$ to $b$ means that integration will be done from the lower limit $a$ and the upper limit $b$ . Also take care when you take the cube roots while finding the final value of $\lambda $, we have written the cube roots as raising the fraction or number to the power of $\dfrac{1}{3}$ . Students can make the mistake while solving the terms raised with power so one must learn the properties of powers.