Questions & Answers
Question
Answers
Related Questions
Let \[P\] be a point on the parabola \[{{y}^{2}}-2y-4x+5=0\], such that the tangent on the parabola at \[P\] intersects the directrix at a point \[Q\]. Let \[R\] be the point that divides the line segment \[QP\] externally in the ratio \[\dfrac{1}{2}:1\]. Find the locus of \[R\].
Answer
![Verified]()
Verified
Verified
Hint: Write the equation of tangent, get points \[Q\] and \[P\] and then use \[x=\dfrac{m{{x}_{2}}-n{{x}_{1}}}{m-n}\] and \[y=\dfrac{m{{y}_{2}}-n{{y}_{1}}}{m-n}\].
We are given a point \[P\] on the parabola \[{{y}^{2}}-2y-4x+5=0\] such that tangent on the parabola at \[P\] intersect the directrix at \[Q\].
We have to find the locus of \[R\] which divides \[QP\] externally in the ratio \[\dfrac{1}{2}:1\].
First of all, we will convert the parabola into its standard form
We take, \[{{y}^{2}}-2y-4x+5=0\]
Or, \[{{y}^{2}}-2y=4x-5\]
Adding \[1\] on both sides,
We get, \[{{y}^{2}}-2y+1=4x-5+1\]
Since we know that \[{{a}^{2}}+{{b}^{2}}-2ab={{\left( a-b \right)}^{2}}\]
Therefore, we get \[{{\left( y-1 \right)}^{2}}=4x-4\]
Or, \[{{\left( y-1 \right)}^{2}}=4\left( x-1 \right)\]
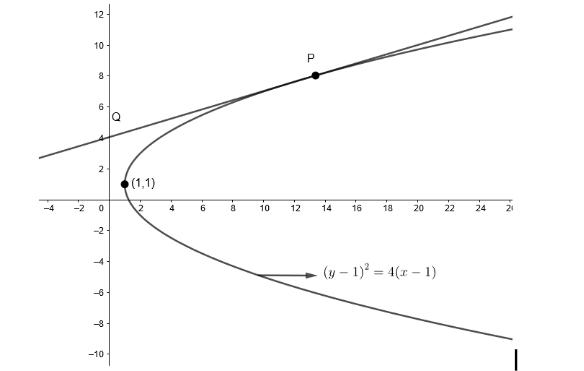
Let \[y-1=Y\] and \[x-1=X\]
So, we get parabola \[{{Y}^{2}}=4X\] which is the standard form of a parabola.
Now, we know that any general point on the parabola is \[\left( a{{t}^{2}},2at \right)\].
By comparing parabola \[{{Y}^{2}}=4X\] with general parabola \[{{y}^{2}}=4ax\],
We get \[4a=4\]
Therefore, we get \[a=1\]
Now, we know that any general point on the parabola \[{{y}^{2}}=4ax\] is \[\left( a{{t}^{2}},2at \right)\]
Since, \[a=1\]
We get, \[P\left( X,Y \right)=P\left( {{t}^{2}},2t \right)\]
We know that tangent at point \[\left( a{{t}^{2}},2at \right)\] is given by \[ty=x+a{{t}^{2}}\]
Since \[a=1\], we get equation of tangent at \[P\left( {{t}^{2}},2t \right)\] as \[tY=X+{{t}^{2}}....\left( i \right)\]
We know that equation of directrix is
\[X=-a\]
Therefore, we get \[X=-1\]
Or, \[X+1=0\]
Since we know that \[Q\] is a point of intersection of tangents and directrix is \[X=-1\].
Therefore, we will put \[X=-1\] in the equation \[\left( i \right)\] to find the \[Y\] coordinate.
So, \[tY=X+{{t}^{2}}\]
\[\Rightarrow tY=-1+{{t}^{2}}\]
\[Y=\dfrac{{{t}^{2}}-1}{t}\]
Therefore, we get a point \[Q\left( X,Y \right)=\left( -1,\dfrac{{{t}^{2}}-1}{t} \right)\]
Let the point \[R\] be \[\left( h,k \right)\] which divides \[QP\] externally in the ratio \[\dfrac{1}{2}:1\]
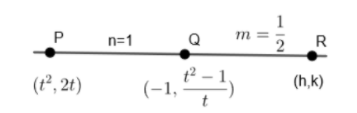
We know that if \[R\left( x,y \right)\] divides \[Q\left( {{x}_{1}},{{y}_{1}} \right)\] and \[P\left( {{x}_{2}},{{y}_{2}} \right)\]in the ratio \[m:n\]
Then, \[x=\dfrac{m\left( {{x}_{2}} \right)-n\left( {{x}_{1}} \right)}{\left( m-n \right)}\]
\[y=\dfrac{m\left( {{y}_{2}} \right)-n\left( {{y}_{1}} \right)}{\left( m-n \right)}\]
Here, we have \[R\left( x,y \right)=\left( h,k \right)\]
\[Q\left( {{x}_{1}},{{y}_{1}} \right)=\left( -1,\dfrac{{{t}^{2}}-1}{t} \right)\]
\[P\left( {{x}_{2}},{{y}_{2}} \right)=\left( {{t}^{2}},2t \right)\]
\[m=\dfrac{1}{2},n=1\]
So, we get \[h=\dfrac{\dfrac{1}{2}\left( {{t}^{2}} \right)-1\left( -1 \right)}{\dfrac{1}{2}-1}\]
\[h=\dfrac{\dfrac{{{t}^{2}}}{2}+1}{\dfrac{-1}{2}}\]
\[h=-\left( {{t}^{2}}+2 \right)\]
Or \[{{t}^{2}}=-2-h....\left( ii \right)\]
And \[k=\dfrac{\dfrac{1}{2}\left( 2t \right)-1\left( \dfrac{{{t}^{2}}-1}{t} \right)}{\dfrac{1}{2}-1}\]
\[k=\dfrac{t-\left( \dfrac{{{t}^{2}}}{t}-\dfrac{1}{t} \right)}{\dfrac{-1}{2}}\]
\[k=-2\left[ t-\left( t-\dfrac{1}{t} \right) \right]\]
\[k=\dfrac{-2}{t}\]
By squaring both the sides,
We get, \[{{k}^{2}}=\dfrac{4}{{{t}^{2}}}\]
Now, by putting the value of \[{{t}^{2}}\] from equation \[\left( ii \right)\]
We get \[{{k}^{2}}=\dfrac{4}{\left( -2-h \right)}\]
By cross multiplying, we get
\[\Rightarrow -{{k}^{2}}\left( h+2 \right)=4\]
To get the locus, we will replace \[h\]by \[X\] and \[k\]by \[Y\].
We get, \[-{{Y}^{2}}\left( X+2 \right)=4\]
As we had assumed that \[X=x-1\] and \[Y=y-1\]
We get, \[-{{\left( y-1 \right)}^{2}}\left( x-1+2 \right)=4\]
\[-{{\left( y-1 \right)}^{2}}\left( x+1 \right)=4\]
Or, \[{{\left( y-1 \right)}^{2}}\left( x+1 \right)+4=0\]
Note: Always convert the given parabola into standard parabola \[{{y}^{2}}=4ax\] and then use the general equation of tangents, normals etc. Also, students often forget to convert \[X\] to \[x\] and \[Y\] to \[y\] and get wrong answers. So this step must be kept in mind.
We are given a point \[P\] on the parabola \[{{y}^{2}}-2y-4x+5=0\] such that tangent on the parabola at \[P\] intersect the directrix at \[Q\].
We have to find the locus of \[R\] which divides \[QP\] externally in the ratio \[\dfrac{1}{2}:1\].
First of all, we will convert the parabola into its standard form
We take, \[{{y}^{2}}-2y-4x+5=0\]
Or, \[{{y}^{2}}-2y=4x-5\]
Adding \[1\] on both sides,
We get, \[{{y}^{2}}-2y+1=4x-5+1\]
Since we know that \[{{a}^{2}}+{{b}^{2}}-2ab={{\left( a-b \right)}^{2}}\]
Therefore, we get \[{{\left( y-1 \right)}^{2}}=4x-4\]
Or, \[{{\left( y-1 \right)}^{2}}=4\left( x-1 \right)\]
Let \[y-1=Y\] and \[x-1=X\]
So, we get parabola \[{{Y}^{2}}=4X\] which is the standard form of a parabola.
Now, we know that any general point on the parabola is \[\left( a{{t}^{2}},2at \right)\].
By comparing parabola \[{{Y}^{2}}=4X\] with general parabola \[{{y}^{2}}=4ax\],
We get \[4a=4\]
Therefore, we get \[a=1\]
Now, we know that any general point on the parabola \[{{y}^{2}}=4ax\] is \[\left( a{{t}^{2}},2at \right)\]
Since, \[a=1\]
We get, \[P\left( X,Y \right)=P\left( {{t}^{2}},2t \right)\]
We know that tangent at point \[\left( a{{t}^{2}},2at \right)\] is given by \[ty=x+a{{t}^{2}}\]
Since \[a=1\], we get equation of tangent at \[P\left( {{t}^{2}},2t \right)\] as \[tY=X+{{t}^{2}}....\left( i \right)\]
We know that equation of directrix is
\[X=-a\]
Therefore, we get \[X=-1\]
Or, \[X+1=0\]
Since we know that \[Q\] is a point of intersection of tangents and directrix is \[X=-1\].
Therefore, we will put \[X=-1\] in the equation \[\left( i \right)\] to find the \[Y\] coordinate.
So, \[tY=X+{{t}^{2}}\]
\[\Rightarrow tY=-1+{{t}^{2}}\]
\[Y=\dfrac{{{t}^{2}}-1}{t}\]
Therefore, we get a point \[Q\left( X,Y \right)=\left( -1,\dfrac{{{t}^{2}}-1}{t} \right)\]
Let the point \[R\] be \[\left( h,k \right)\] which divides \[QP\] externally in the ratio \[\dfrac{1}{2}:1\]
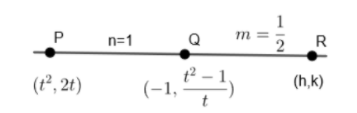
We know that if \[R\left( x,y \right)\] divides \[Q\left( {{x}_{1}},{{y}_{1}} \right)\] and \[P\left( {{x}_{2}},{{y}_{2}} \right)\]in the ratio \[m:n\]
Then, \[x=\dfrac{m\left( {{x}_{2}} \right)-n\left( {{x}_{1}} \right)}{\left( m-n \right)}\]
\[y=\dfrac{m\left( {{y}_{2}} \right)-n\left( {{y}_{1}} \right)}{\left( m-n \right)}\]
Here, we have \[R\left( x,y \right)=\left( h,k \right)\]
\[Q\left( {{x}_{1}},{{y}_{1}} \right)=\left( -1,\dfrac{{{t}^{2}}-1}{t} \right)\]
\[P\left( {{x}_{2}},{{y}_{2}} \right)=\left( {{t}^{2}},2t \right)\]
\[m=\dfrac{1}{2},n=1\]
So, we get \[h=\dfrac{\dfrac{1}{2}\left( {{t}^{2}} \right)-1\left( -1 \right)}{\dfrac{1}{2}-1}\]
\[h=\dfrac{\dfrac{{{t}^{2}}}{2}+1}{\dfrac{-1}{2}}\]
\[h=-\left( {{t}^{2}}+2 \right)\]
Or \[{{t}^{2}}=-2-h....\left( ii \right)\]
And \[k=\dfrac{\dfrac{1}{2}\left( 2t \right)-1\left( \dfrac{{{t}^{2}}-1}{t} \right)}{\dfrac{1}{2}-1}\]
\[k=\dfrac{t-\left( \dfrac{{{t}^{2}}}{t}-\dfrac{1}{t} \right)}{\dfrac{-1}{2}}\]
\[k=-2\left[ t-\left( t-\dfrac{1}{t} \right) \right]\]
\[k=\dfrac{-2}{t}\]
By squaring both the sides,
We get, \[{{k}^{2}}=\dfrac{4}{{{t}^{2}}}\]
Now, by putting the value of \[{{t}^{2}}\] from equation \[\left( ii \right)\]
We get \[{{k}^{2}}=\dfrac{4}{\left( -2-h \right)}\]
By cross multiplying, we get
\[\Rightarrow -{{k}^{2}}\left( h+2 \right)=4\]
To get the locus, we will replace \[h\]by \[X\] and \[k\]by \[Y\].
We get, \[-{{Y}^{2}}\left( X+2 \right)=4\]
As we had assumed that \[X=x-1\] and \[Y=y-1\]
We get, \[-{{\left( y-1 \right)}^{2}}\left( x-1+2 \right)=4\]
\[-{{\left( y-1 \right)}^{2}}\left( x+1 \right)=4\]
Or, \[{{\left( y-1 \right)}^{2}}\left( x+1 \right)+4=0\]
Note: Always convert the given parabola into standard parabola \[{{y}^{2}}=4ax\] and then use the general equation of tangents, normals etc. Also, students often forget to convert \[X\] to \[x\] and \[Y\] to \[y\] and get wrong answers. So this step must be kept in mind.
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
-
Courses-
Crash Courses 2021
-
Olympiads/NTSE/Others
-
Micro Courses
-
Vedantu Super Kids NEW
-
Reading & Spoken English -
FREEMaster Classes
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
