Question

Let $\overrightarrow n $ be a vector of magnitude $3\sqrt 3 $ such that it makes equal acute angles with the coordinate axes. Find the vector equation and also cartesian form of the equation of a plane passing through $\left( { - 1,1,2} \right)$ and normal to $\overrightarrow n $.

Answer 1

Hint:
We will first find the value of cosine of angle made by the vector with the $x$ axis using the given condition and the property that ${\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = 1$, where $\alpha ,\beta ,\gamma $ are the angles made by the vector with the $x,y,z$ axis respectively. Then, find the value of vector $\overrightarrow n $. Next, represent the equation of plane in vector form as $\left( {\overrightarrow r - \overrightarrow p } \right).\overrightarrow n = 0$, where $\overrightarrow r $ is any vector on plane, $\overrightarrow p $ is the vector represented by the given point.

Complete step by step solution:
Let the vector $\overrightarrow n $ makes angle $\alpha ,\beta ,\gamma $ be acute angles made with $x,y,z$ axis respectively.
Now, we know that the square of the sum of cosines of the angles made by the vector with each axis is equal to 1
That is, ${\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = 1$
We are given that all the angles are equal, then $\alpha = \beta = \gamma $
Hence, we will have
$
  {\cos ^2}\alpha + {\cos ^2}\alpha + {\cos ^2}\alpha = 1 \\
   \Rightarrow 3{\cos ^2}\alpha = 1 \\
   \Rightarrow {\cos ^2}\alpha = \dfrac{1}{3} \\
   \Rightarrow \cos \alpha = \pm \dfrac{1}{{\sqrt 3 }} \\
$
But, $\alpha $ is an acute angle, then,
$\cos \alpha = \dfrac{1}{{\sqrt 3 }}$
The vector $\overrightarrow n $ can be calculated using the property,
\[\overrightarrow n = \left| {\overrightarrow n } \right|\left( {\cos \alpha \hat i + \cos \beta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} + \cos \gamma \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} } \right)\]
We are also given that the magnitude of the vector $\overrightarrow n $ is $3\sqrt 3 $
And each of the angle is equal with the value $\cos \alpha = \dfrac{1}{{\sqrt 3 }}$
Then, we will have,

$
  \overrightarrow n = 3\sqrt 3 \left( {\dfrac{1}{{\sqrt 3 }}\hat i + \dfrac{1}{{\sqrt 3 }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} + \dfrac{1}{{\sqrt 3 }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} } \right) \\
   \Rightarrow \overrightarrow n = 3\left( {\hat i + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} } \right) \\
$
Therefore, the vector $\overrightarrow n = 3\hat i + 3\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} + 3\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} $
But, we have to find the equation of the plane , where the plane passes through $\left( { - 1,1,2} \right)$
Let $\overrightarrow r = x\hat i + y\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} + z\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} $ be any vector on the plane and the vector represented by the given point be $\overrightarrow p = - \hat i + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} + 2\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} $
Also, vector $\overrightarrow n $ has to normal to the plane.
Then, $\left( {\overrightarrow r - \overrightarrow p } \right).\overrightarrow n = 0$ represents the required plane.
On substituting the values in the above formula, we will get,
$
  \left( {\left( {x\hat i + y\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} + z\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} } \right) - \left( { - \hat i + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} + 2\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} } \right)} \right).\left( {3\hat i + 3\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} + 3\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} } \right) = 0 \\
   \Rightarrow \left( {\left( {x + 1} \right)\hat i + \left( {y - 1} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} + \left( {z - 2} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} } \right).\left( {3\hat i + 3\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} + 3\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} } \right) = 0 \\
   \Rightarrow 3\left( {x + 1} \right) + 3\left( {y - 1} \right) + 3\left( {z - 2} \right) = 0 \\
$
On simplifying the above brackets, we will get,
$
  3\left( {x + 1} \right) + 3\left( {y - 1} \right) + 3\left( {z - 2} \right) = 0 \\
   \Rightarrow 3x + 3 + 3y - 3 + 3z - 6 = 0 \\
   \Rightarrow 3x + 3y + 3z - 6 = 0 \\
   \Rightarrow x + y + z - 2 = 0 \\
$

Hence, the equation of the plane in the cartesian form is $x + y + z - 2 = 0$

Note:

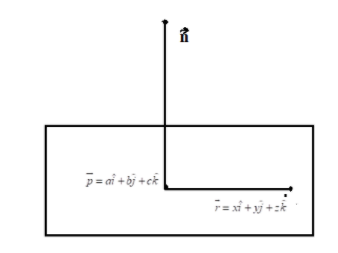
If there is a plane and let $\overrightarrow r = x\hat i + y\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} + z\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} $ be any vector on plane and plane is passing through $P\left( {a,b,c} \right)$ which can be represented as $\overrightarrow p = a\hat i + b\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} + c\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} $ , and there is a normal $\overrightarrow n $ to the plane, then the equation of plane is given as $\left( {\overrightarrow r - \overrightarrow p } \right).\overrightarrow n = 0$