Question

Let $\Gamma $ denote a curve y = f(x) which is in the first quadrant and let the point (1, 0) lie on it. Let the tangent to $\Gamma $ at a point P intersect the y – axis at ${{\text{Y}}_{p}}$. If $\text{P}{{\text{Y}}_{p}}$ has length 1 for each point P on $\Gamma $. Then which of the following options is/are correct?
(This question has multiple correct options)
(a) $y=-\ln \left( \dfrac{1+\sqrt{1-{{x}^{2}}}}{x} \right)+\sqrt{1-{{x}^{2}}}$
(b) $xy'+\sqrt{1-{{x}^{2}}}=0$
(c) $xy'-\sqrt{1-{{x}^{2}}}=0$
(d) $y=\ln \left( \dfrac{1+\sqrt{1-{{x}^{2}}}}{x} \right)+\sqrt{1-{{x}^{2}}}$

Answer 1

Hint: To solve this question, we will take some point P(m, n) such that it lies on the curve y = f(x). Then we will find the equation of the tangent to the curve y = f(x) from point P in slope point form. The slope of this tangent will be equal to first order differential of the curve at point P. We know that this tangent intersects the y – axis at the point ${{\text{Y}}_{p}}$. But substituting x = 0 in the equation of tangent, we can find point ${{\text{Y}}_{p}}$. Now we know that the segment $\text{P}{{\text{Y}}_{p}}$ has a length of 1. Thus, we will use distance formula and equate it to 1. This will give us a differential equation. Once we solve the differential equation, we will find the equation of the curve. Then we will see which of the options satisfy with the equation.

Complete step-by-step answer:

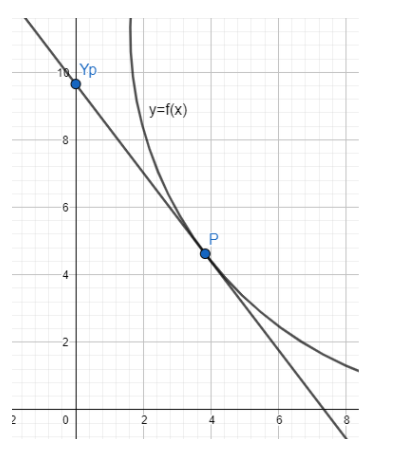
Let the coordinates of the point P on the curve be (m, n), such that f(m) = n.
The equation of the tangent at point P to the curve y = f(x) will in the slope point form will be as follows:
$\Rightarrow y-n=\dfrac{dy}{dx}\left( x-m \right)$
We know that this line intersects the y – axis at point ${{\text{Y}}_{p}}$. To find the coordinates of the point ${{\text{Y}}_{p}}$, we will substitute x = 0.
$\begin{align}
  & \Rightarrow y-n=\dfrac{dy}{dx}\left( 0-m \right) \\
 & \Rightarrow y=n+m\dfrac{dy}{dx} \\
\end{align}$
Thus, coordinates of point ${{\text{Y}}_{p}}$ be $\left( 0,n+m\dfrac{dy}{dx} \right)$ .
We also know that the distance ($\text{P}{{\text{Y}}_{p}}$) = 1
\[\begin{align}
  & \Rightarrow \sqrt{{{\left( n+m\dfrac{dy}{dx}-n \right)}^{2}}+{{\left( 0-m \right)}^{2}}}=1 \\
 & \Rightarrow {{\left( m\dfrac{dy}{dx} \right)}^{2}}+{{m}^{2}}=1 \\
 & \Rightarrow {{m}^{2}}\left( {{\left( \dfrac{dy}{dx} \right)}^{2}}+1 \right)=1 \\
 & \Rightarrow {{\left( \dfrac{dy}{dx} \right)}^{2}}=\dfrac{1-{{m}^{2}}}{{{m}^{2}}} \\
 & \Rightarrow \dfrac{dy}{dx}=\pm \dfrac{\sqrt{1-{{m}^{2}}}}{m} \\
\end{align}\]
Now, that the (m, n) lies on the curve y = f(x), we will replace m = x and n = y.
\[\Rightarrow dy=\pm \dfrac{\sqrt{1-{{x}^{2}}}}{x}dx\]
This is a differential equation. To find the curve, we will integrate both sides.
\[\Rightarrow \int{dy}=\pm \int{\dfrac{\sqrt{1-{{x}^{2}}}}{x}dx}\]
To solve the integral on the right-hand side, we will substitute x = $\sin \theta $
$\Rightarrow dx=\cos \theta d\theta $
\[\begin{align}
  & \Rightarrow y=\pm \int{\dfrac{\cos \theta }{\sin \theta }\cos \theta d\theta } \\
 & \Rightarrow y=\pm \int{\dfrac{1-{{\sin }^{2}}\theta }{\sin \theta }d\theta } \\
 & \Rightarrow y=\pm \int{\left( \cos \text{ec}\theta -\sin \theta \right)d\theta } \\
 & \Rightarrow y=\pm \left[ -\ln \left( \cos \text{ec}\theta +\cot \theta \right)+\cos \theta \right]+C \\
 & \Rightarrow y=\pm \left[ -\ln \left( \dfrac{1+\sqrt{1-{{x}^{2}}}}{x} \right)+\sqrt{1-{{x}^{2}}} \right]+C \\
\end{align}\]
We know that the curve is in the first quadrant, so y must be positive.
\[\begin{align}
  & \Rightarrow y=-\left[ -\ln \left( \dfrac{1+\sqrt{1-{{x}^{2}}}}{x} \right)+\sqrt{1-{{x}^{2}}} \right]+C \\
 & \Rightarrow y=\ln \left( \dfrac{1+\sqrt{1-{{x}^{2}}}}{x} \right)-\sqrt{1-{{x}^{2}}}+C \\
\end{align}\]
We know that (1, 0) lies on the curve. So, if we substitute x = 1, y = 0
\[\begin{align}
  & \Rightarrow \left( 0 \right)=\ln \left( \dfrac{1+\sqrt{1-1}}{1} \right)-\sqrt{1-0}+C \\
 & \Rightarrow C=0 \\
\end{align}\]
Therefore, the equation of the curve is \[y=\ln \left( \dfrac{1+\sqrt{1-{{x}^{2}}}}{x} \right)-\sqrt{1-{{x}^{2}}}\] .
In the equation \[\dfrac{dy}{dx}=\pm \dfrac{\sqrt{1-{{m}^{2}}}}{m}\], the correct sign is ( ─ ).
\[\dfrac{dy}{dx}=-\dfrac{\sqrt{1-{{m}^{2}}}}{m}\]
Substitute m = x, as (m, n) is a point on the curve.
\[\begin{align}
  & \Rightarrow xy'=-\sqrt{1-{{x}^{2}}} \\
 & \Rightarrow xy'+\sqrt{1-{{x}^{2}}}=0 \\
\end{align}\]
Hence, option (b) and option (d) are correct answers.

Note: This is an advanced level question and students are advised to be well versed in differential equations, integration and coordinate geometry to be able to solve this question. Moreover, it is always advisable to draw the figure.