Question

Let \[{E_1}\] and \[{E_2}\] be two ellipses whose centers are at origin. The major axes of \[{E_1}\] and \[{E_2}\] lie along the x-axis and y-axis, respectively. Let S be the circle \[{x^2} + {(y - 1)^2} = 2\]. The straight line \[x + y = 3\] touches the curves S, \[{E_1}\] and \[{E_2}\] at P, Q and R, respectively. Suppose that \[PQ = PR = \dfrac{{2\sqrt 2 }}{3}\] . If \[{e_1}\]and \[{e_2}\]are the eccentricities of \[{E_1}\]and \[{E_2}\], respectively then the correct expression(s) is (are)

THIS QUESTION HAS MULTIPLE CORRECT OPTIONS

A.\[{e_1}^2 + {e_2}^2 = \dfrac{{43}}{{40}}\]

B.\[{e_1}{e_2} = \dfrac{{\sqrt 7 }}{{2\sqrt {10} }}\]

C.\[|{e_1}^2 - {e_2}^2| = \dfrac{5}{8}\]

D.\[{e_1}{e_2} = \dfrac{{\sqrt 3 }}{4}\]

Answer 1

Hint: Firstly we write the parametric points to both the ellipse with the condition of \[PQ = PR = \dfrac{{2\sqrt 2 }}{3}\], then we calculate the random point touching on the line and the circle, hence we derive the parametric point from there for line and so calculate the random points values using \[PQ = PR = \dfrac{{2\sqrt 2 }}{3}\]and hence on the comparison, we can get the values through which equation or ellipse can be written. And hence once the equation of ellipse is obtained we can determine it’s eccentricity using formula as \[e = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}} \]. And then after getting the value of both the eccentricity we can check for the above options.

Complete step-by-step answer:
The givens equation of the circle \[{x^2} + {(y - 1)^2} = 2\] and the straight line is \[x + y = 3\].

Now, let the general equation for both the ellipse be

\[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\]and \[\dfrac{{{x^2}}}{{{A^2}}} + \dfrac{{{y^2}}}{{{B^2}}} = 1\]

So, we know that the distances \[PQ = PR = \dfrac{{2\sqrt 2 }}{3}\]

Diagram:

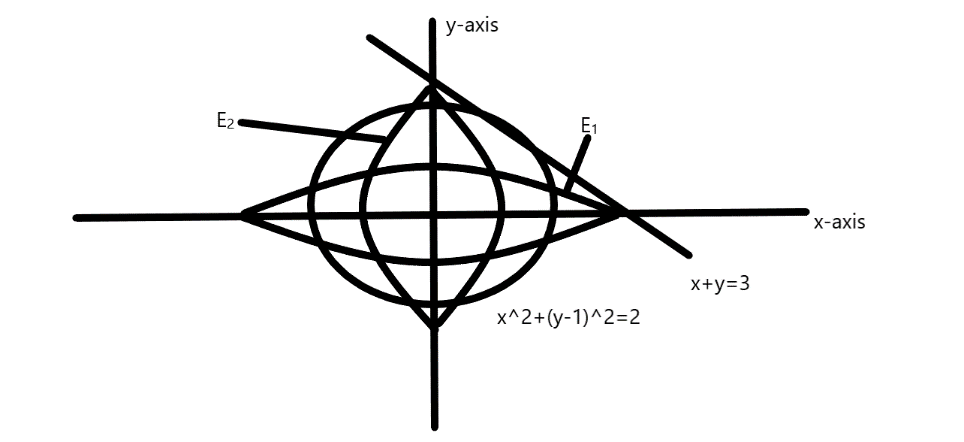
Hence, considering the general point of contact for both the ellipses can be given as,

\[(\dfrac{{{a^2}}}{3},\dfrac{{{b^2}}}{3})\]and for another ellipse point of contact will be given as \[(\dfrac{{{A^2}}}{3},\dfrac{{{B^2}}}{3})\].

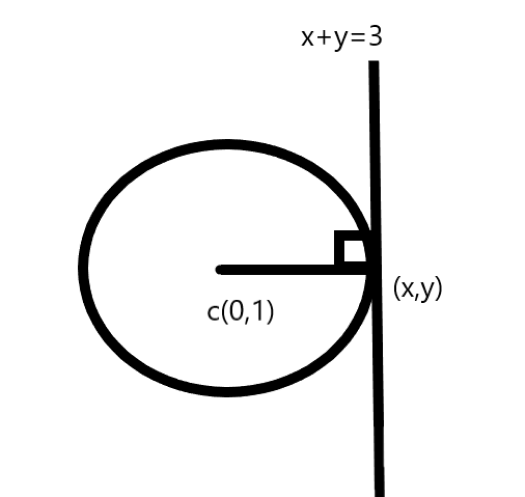
Now, considering the condition for circle and the straight line as,

The equation of straight line is \[x + y = 3\]and the centre of circle is \[(0,1)\]

Calculating their point of intersection of the circle and straight line,

Diagram of the circle and straight line:
 

Calculate the equation of line connecting contact point and centre, apply the conditions that if the slopes are perpendicular then the equation among slopes can be given as \[{m_1}.{m_2} = - 1\]. And if needed also apply the distance formula among the among the centre and the contact point and equate it to the radius as
 \[\sqrt {{{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{x_2} - {x_1}} \right)}^2}} = r\].

Hence, first calculating the slope of line using \[{m_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\] is given as,

\[{m_1} = \dfrac{{y - 1}}{x}\]

And now use the equation of \[{m_1}.{m_2} = - 1\]

\[ \Rightarrow \]\[\dfrac{{y - 1}}{x}.\left( { - 1} \right) = - 1\] as slope of given line is \[x + y = 3\].

Hence the equation can be formed as

\[ \Rightarrow \]\[y = x + 1\]

Now, also use the concept of distance formula as \[\sqrt {{{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{x_2} - {x_1}} \right)}^2}} = r\]

And so it can be given as\[{\left( {y - 1} \right)^2} + {\left( x \right)^2} = 2\]

On expanding the above equation as

\[ \Rightarrow \]\[{x^2} + {y^2} - 2y = 1\]

Hence, we need to search for point of intersection of both point from the equation \[{x^2} + {y^2} - 2y = 1\] and \[y = x + 1\]

Hence, point of intersection will be \[\left( {1,2} \right)\]

So, using the above-given information as writing the parametric points of distances and using it with the given conditions can be done as,

Let the parametric points for one coordinate of\[\left( {\dfrac{{{a^2}}}{3},\dfrac{{{b^2}}}{3}} \right)\]be given as \[\left( {1 + \dfrac{r}{{\sqrt 2 }},2 - \dfrac{r}{{\sqrt 2 }}} \right)\],where r is the distance among the

Calculated and the given point which is given by \[r = PQ = PR = \dfrac{{2\sqrt 2 }}{3}\].

Hence, \[\left( {\dfrac{{{a^2}}}{3},\dfrac{{{b^2}}}{3}} \right) = \left( {1 + \dfrac{{2\sqrt 2 }}{{3\sqrt 2 }},2 - \dfrac{{2\sqrt 2 }}{{3\sqrt 2 }}} \right)\]

Hence, on comparison we can calculate the value of \[{a^2}\],\[{b^2}\]as point is \[\left( {\dfrac{5}{3},\dfrac{4}{3}} \right)\]

Hence, \[{a^2} = 5,{b^2} = 4\]

Let the parametric points for another coordinate of \[\left( {\dfrac{{{A^2}}}{3},\dfrac{{{B^2}}}{3}} \right)\] be given as \[\left( {1 - \dfrac{r}{{\sqrt 2 }},2 + \dfrac{r}{{\sqrt 2 }}} \right)\], where r is the distance among the

Calculated and the given point which is given by \[r = PQ = PR = \dfrac{{2\sqrt 2 }}{3}\].

Hence, \[\left( {\dfrac{{{A^2}}}{3},\dfrac{{{B^2}}}{3}} \right) = \left( {1 - \dfrac{{2\sqrt 2 }}{{3\sqrt 2 }},2 + \dfrac{{2\sqrt 2 }}{{3\sqrt 2 }}} \right)\]

Hence, on comparison we can calculate the value of \[{A^2}\], \[{B^2}\] as point is \[\left( {\dfrac{1}{3},\dfrac{8}{3}} \right)\]

Hence, \[{A^2} = 1,{B^2} = 8\]

Hence, now as we know all the values and equation of ellipse can be now given as

\[\dfrac{{{x^2}}}{5} + \dfrac{{{y^2}}}{4} = 1\] and \[\dfrac{{{x^2}}}{1} + \dfrac{{{y^2}}}{8} = 1\]

Hence, eccentricity of the ellipse can be calculated using the formula of \[e = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}} \]

Hence, calculate both the eccentricities as,

For, \[\dfrac{{{x^2}}}{5} + \dfrac{{{y^2}}}{4} = 1\], \[{e_1} = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}} \] hence, put the values

\[ \Rightarrow \]\[{e_1} = \sqrt {1 - \dfrac{4}{5}} \]

On simplifying further,

\[
   = \sqrt {\dfrac{{5 - 4}}{5}} \\
   = \sqrt {\dfrac{1}{5}} \\
 \]

Similarly, for another ellipse

For, \[\dfrac{{{x^2}}}{1} + \dfrac{{{y^2}}}{8} = 1\], \[{e_1} = \sqrt {1 - \dfrac{{{A^2}}}{{{B^2}}}} \] hence, put the values

\[ \Rightarrow \]\[{e_2} = \sqrt {1 - \dfrac{1}{8}} \]

On simplifying further,

\[
   = \sqrt {\dfrac{{8 - 1}}{5}} \\
   = \sqrt {\dfrac{7}{8}} \\
 \]

Now, as both the eccentricities are known, but the values in the option and check for the correct answer.
Hence, \[
  {e_1}^2 = \dfrac{1}{5} \\
  {e_2}^2 = \dfrac{7}{8} \\
 \]

So checking all the given option individually as,

\[{e_1}^2 + {e_2}^2 = \dfrac{1}{5} + \dfrac{7}{8}\]

Hence, on simplifying

\[ \Rightarrow \]\[{e_1}^2 + {e_2}^2 = \dfrac{{43}}{{40}}\]………(1)

Now, \[{e_1}.{e_2} = \sqrt {\dfrac{1}{5}} .\sqrt {\dfrac{7}{8}} \]

On simplification further, it can be given as

\[ \Rightarrow \]\[{e_1}.{e_2} = \dfrac{1}{2}\sqrt {\dfrac{7}{{10}}} \]………(2)

Hence now checking to option of \[|{e_1}^2 - {e_2}^2| = \dfrac{5}{8}\]

On putting the values as,

\[ \Rightarrow \]\[|{e_1}^2 - {e_2}^2| = \]\[\left| {\dfrac{1}{5} - \dfrac{7}{8}} \right| = \left| {\dfrac{{8 - 35}}{{40}}} \right|\]

On simplifying, we can see that

\[|{e_1}^2 - {e_2}^2| = \dfrac{{27}}{{40}}\]………..(3)

Hence from (1) and (2), we have that Option (A) and (B) are correct.

Note: In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. As such, it generalizes a circle, which is the special type of ellipse in which the two focal points are the same.
A circle is a shape consisting of all points in a plane that are a given distance from a given point, the centre; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant.
In geometry, the notion of line or straight line was introduced by ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects, which are often described in terms of two points or referred to using a single letter.