Question

Let ABCD is parallelogram such that \[\overline {AB} = \overrightarrow q ,\overline {AD} = \overrightarrow p {\text{ and }}\angle BAD\] be an acute angle. If $\overrightarrow r $ is the vector coincides with the altitude directed from the vertex \[B\] to the side $AD$, then $\overrightarrow r $ is given by:
\[
  {\text{(A) }}\overrightarrow r = 3\overrightarrow q - \dfrac{{3(\overrightarrow p .\overrightarrow q )}}{{\overrightarrow p .\overrightarrow p }}\overrightarrow p \\
  {\text{(B) }}\overrightarrow r = - \overrightarrow q + \left( {\dfrac{{\overrightarrow p .\overrightarrow q }}{{\overrightarrow p .\overrightarrow p }}} \right)\overrightarrow p \\
  {\text{(C) }}\overrightarrow r = \overrightarrow q - \left( {\dfrac{{\overrightarrow p .\overrightarrow q }}{{\overrightarrow p .\overrightarrow p }}} \right)\overrightarrow p \\
  {\text{(D) }}\overrightarrow r = - 3\overrightarrow q + \dfrac{{3(\overrightarrow p .\overrightarrow q )}}{{\overrightarrow p .\overrightarrow p }}\overrightarrow p \\
 \]

Answer 1

Hint:This problem is related to vector geometry. It should be noted here that a dot product of two vectors is a scalar quantity (\[\overrightarrow A .\overrightarrow B = AB\cos \theta ,\] where $\theta $ is the angle between them) and if the vectors are perpendicular to each other their dot product is zero because the value of $\cos {90^ \circ } = 0$. We will use this property of vector products to solve the problem.

Complete step-by-step answer:
Firstly, draw a parallelogram ABCD in such a way that \[\overline {AB} = \overrightarrow q ,\overline {AD} = \overrightarrow p {\text{ and }}\angle BAD\] should be an acute angle. See below,

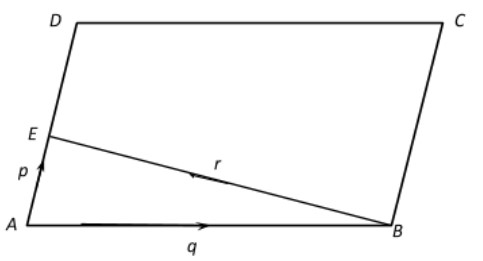
Now, in the diagram, draw a line originating from vertex \[B\] to the side $AD$ in such a way that it should be perpendicular to side $AD$. This way $\Delta AEB$ will be a right angle triangle.
We know that, vector$\overrightarrow r $can be written in the form of vector $\overrightarrow q $ and vector $\overrightarrow p $. Now, from the diagram above, it is known that the direction of vector $\overrightarrow r $is opposite to the direction of vector$\overrightarrow q $. Hence, when we write the vector $\overrightarrow r $ in terms of vector $\overrightarrow q $, we shall have to put a negative sign in front of the vector $\overrightarrow q $.
Now, vector $\overrightarrow p $represents the side $AD$, so assume that $\alpha \overrightarrow p $represents the side $AE$ in $\Delta AEB$. Therefore, now vector $\overrightarrow r $can be written in the form of vector $\overrightarrow q $ and vector $\overrightarrow p $ in the following way,
$\overrightarrow r = - \overrightarrow q + \alpha \overrightarrow p {\text{ }}................(1)$
Now, we know that the dot product to two perpendicular vectors is zero. In this diagram, vector$\overrightarrow r $and vector$\overrightarrow p $ are perpendicular to each other.
Therefore,
$\overrightarrow r .\overrightarrow p = 0$
Putting the value of vector$\overrightarrow r $ from eq. (1) in the above expression, we will get
\[
  \overrightarrow r .\overrightarrow p = 0 \\
   \Rightarrow ( - \overrightarrow q + \alpha \overrightarrow p ).\overrightarrow p = 0 \\
   \Rightarrow - \overrightarrow q .\overrightarrow p + \alpha \overrightarrow p .\overrightarrow p = 0 \\
   \Rightarrow \alpha = \dfrac{{\overrightarrow q .\overrightarrow p }}{{\overrightarrow p .\overrightarrow p }} \\
 \]
Now, putting this value of $\alpha $, we will get the value of vector$\overrightarrow r $as
$\overrightarrow r = - \overrightarrow q + \dfrac{{\overrightarrow q .\overrightarrow p }}{{\overrightarrow p .\overrightarrow p }}\overrightarrow p $

So, the correct answer is “Option B”.

Note:In these types of problems, you should take care while drawing the diagram and putting the vector’s direction. Though, it is not given in the problem that the vector $\overrightarrow r $is perpendicular to$\overrightarrow p $but we have assumed that they are perpendicular to each other so that property of dot product of vectors can be utilised.