Question

Let ABCD be a parallelogram and let E be the mid point of side AB. If EC is perpendicular to ED, then
(a) \[ED=EC\]
(b) \[EB=BC\]
(c) \[EA=ED\]
(d) \[EC+ED=2BC\]

Answer 1

Hint: Consider the properties of parallelogram (we know that $AB\parallel CD\text{ and }AD\parallel BC$ for a parallelogram) to solve the question.

From the figure, consider the parallelogram ABCD.

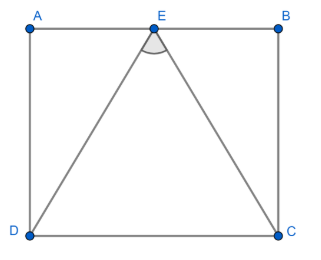
From the properties of parallelogram, we know that $AB\parallel CD\text{ and }AD\parallel BC$
i.e., $AB$ is parallel to $CD$ and
$AD$ is parallel to $BC$
Which can also be considered as sides $AB$ and$DC$ are equal
$AB=DC$
Similarly $AD=BC$
i.e., Both pairs of opposite sides are parallel and they are congruent.
From the figure, it's clear that E is the midpoint of side \[AB.\]
i.e. $AE=EB$
It’s also given that $EC$ is perpendicular to $ED$ and they form an angle of $90{}^\circ $.
i.e., $\angle DEC=90{}^\circ $
In the case of parallelogram $ABCD,\text{ }\angle A=\angle C\text{ and }\angle B=\angle D$ .
From the figure we can find that $ED\ne EC.$ i.e., they are not of the same length.
Which means both $ED\text{ and }EC$are greater than the length $DC$
$\Rightarrow ED>DC\text{ and E}C>DC$
Now adding them together
\[\frac{\begin{align}
  & ED>DC \\
 & ED>DC \\
\end{align}}{ED+EC>2DC}\]
Let us consider that $BC$ is greater than $DC$
$\therefore $ Equation becomes $\Rightarrow ED+EC=2BC.$
So option D is correct.

Note: Remember the properties of parallelogram, with which we have to solve this equation.
As $EC\bot ED,$ students may miscalculate that $EC=ED$ which states that option A is wrong.
From the figure, $EA\ne ED$ i.e., $EA$ is shorter than the length of $ED,$ So option C is wrong.