Question

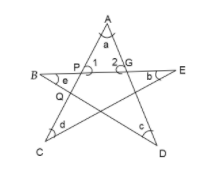
In the star shape shown in figure, the sum of the angle marked at the corners A,B,C,D,E is?
                    

A. 90
B. 135
C. 180
D. 140
E. None of these

Answer 1

Hint: We will solve this question by the sum of triangle. We will solve the question with the help of the angle sum property of a triangle which means the sum of all the angles in the triangle is equal to ${180^ \circ }$.

Complete step-by-step answer:
Let us first take the $\vartriangle PCE$
Angle 1 is exterior angle so, we use the property of exterior angle here
$\angle 1 = \angle b + \angle d$ …………..1
Now, in $\vartriangle BGD$ angle 2 is exterior angle for $\vartriangle BGD$
$\angle 2 = \angle c + \angle e$ ……………2
In $\vartriangle APG$ we know that sum of all the angle of the $\vartriangle APG$ is equal to ${180^ \circ }$
Angles in $\vartriangle APG$ are $\angle a, \angle 1 and \angle 2$
By angle sum property of a triangle
$\angle a + \angle 1 + \angle 2 = {180^{^ \circ }}$
Now, put the value of angle 1 and angle 2 by the equation 1 and 2
$\angle a + \angle d + \angle c + \angle e + \angle b = {180^ \circ }$ \[\]
So, the sum of the all the angles marked at the corners A,B,C,D,E is ${180^ \circ }$

So, the correct answer is “Option C”.

Note: In this question always remember that the angle of each exterior point is always the sum of two adjacent interior angles ${180^ \circ }$.
Alternative method: The adjoining star contains a regular pentagon, and we know the sum of interior angles is $ = {540^ \circ }$, and each angle is of the same measures so we can find the particular angle by dividing the sum by 5.
$ = \dfrac{{540}}{5}$
$ = {108^ \circ }$
It`s supplementary angles measure ${180^ \circ } - {108^ \circ } = {72^ \circ }$
The triangle formed by the star are isosceles triangle in which two angle are $ = {72^ \circ }$
So, we have the find the third angle
=${180^ \circ } - {72^ \circ } - {72^ \circ } = {36^ \circ }$
Each angle at the vertices of the star is equal to ${36^ \circ }$. Thus the sum of all the angle of the star
=${5 \times 36^ \circ } = {180^ \circ }$
Hence the answer is ${180^ \circ }$.
Option C is correct.