Question

In the given graph arrow indicates specifically:

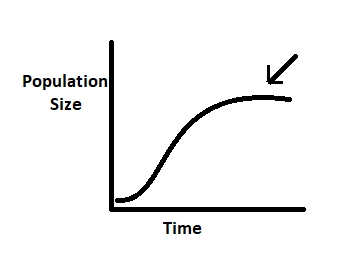
A. r
B. K-N
C. K
D. Density independent effect

Answer 1

Hint: The above graph represents population size v/s time curve. The process of a population's rate of growth slowing as the number of people in the population grows is known as logistic population growth. Here, K is the carrying capacity which is the average population size of the species in a particular habitat.

Complete step-by-step answer:

It is a population growth curve with a logistic or geometric growth pattern.
We can see the graph between population density (N) on the Y-axis and time (t) on the X-axis, which results in a given curve.
The given growth curve represents the relationship between N and t (population density and time) as an exponential or geometric growth of population growth.
As a result, the graph in the diagram represents exponential or geometric increases in the population.
Logistic growth can be thought of as a mathematical equation. The rate of population growth (N) is measured in terms of the total number of people in a population over time (t). The rate of population growth is denoted by $\left ( \dfrac{dN}{dt} \right )$. The d simply represents variation. K represents carrying capacity, and r represents the maximum per capita rate of growth for a population. The word "per capita" refers to an individual, while the per capita growth rate considers both births and deaths in a population. Based on the logistic growth equation, K and r in a population do not change over time.
$\dfrac{dN}{dt}=rN\left ( \dfrac{K-N}{K} \right )$

Hence, the correct option is C

Note: We need to note that logistic growth gives S shape curve whereas exponential growth gives J shaped curve. For population growth to be exponential, the rate of growth must be constant over time.