Question

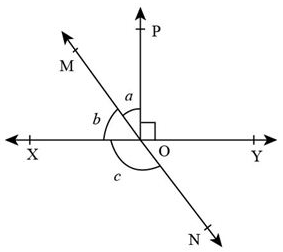
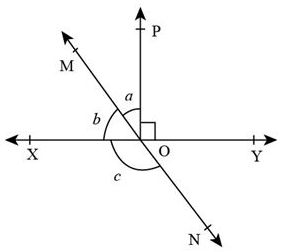
In the given figure, lines XY and MN intersect at O. If $\angle POY = {90^ \circ }$ and a:b = 2 : 3, then $\angle XON$ is equal to……..

A. ${126^ \circ }$
B. ${30^ \circ }$
C. ${90^ \circ }$
D. ${180^ \circ }$

Answer 1

Hint:For solving this question, we use the concept of linear pair of angles. We will use axiom1 of linear pair of angles for finding out the value of a and b. As given a:b = 2:3, a = 2x, b = 3x, adding a and b and $\angle POY$sum should be equal to \[{180^ \circ }\]. Similarly applying axiom1 on b and c we will be able to find the value of angle $\angle XON$.

Complete step-by-step answer:
Linear pair of angles: If non common arms of two adjacent angles form a line, then these angles are called linear pairs of angles. There are basically two axioms for linear pair of angles known as linear pair axioms they are as follow:
Axiom1: If a ray stands on a line, then the sum of two adjacent angles so formed is 180°i.e, the sum of the linear pair is 180°. Axiom2: If the sum of two adjacent angles is 180° then the two non common arms of the angles form a line.

Given,
$\angle POY = {90^ \circ }\,\,\,\,\,\, \ldots ..{\text{ }}\left( 1 \right)$
$a:b = 2:3\,\,\,\,\,\,\, \ldots ..{\text{ }}\left( 2 \right)$
Let the common ratio between a and b be x, therefore, a = 2x, b = 3x.
According to the question: $\angle POY + \angle POX = {180^ \circ }\,\,\,\,\,\,\, \ldots ..{\text{ }}\left( 3 \right)$ [By linear pair axiom]
Given, $\angle POX = a + b\,\,\,\,\, \ldots ..{\text{ }}\left( 4 \right)$
Substituting equation (4) in equation (3), we get,
\[ \Rightarrow \angle POY\; + {\text{ }}a{\text{ }} + {\text{ }}b{\text{ }} = {\text{ }}{180^ \circ }\,\,\,\,\, \ldots ..{\text{ }}\left( 5 \right)\]
Substituting equation (1) in equation (5), we get,
\[ \Rightarrow 90^\circ + {\text{ }}a{\text{ }} + {\text{ }}b{\text{ }} = {\text{ }}{180^ \circ }\]
\[ \Rightarrow a{\text{ }} + {\text{ }}b{\text{ }} = {\text{ }}{90^ \circ }\] $.....(6)$
Substituting value of a = 2x and b =3x in equation (6), we get,
\[\begin{array}{*{20}{l}}
  { \Rightarrow 5x{\text{ }} = {\text{ }}{{90}^ \circ }} \\
  { \Rightarrow x{\text{ }} = {\text{ }}{{18}^ \circ }}
\end{array}\]
Therefore,
$ \Rightarrow a = 2x = 2({18^ \circ }) = {36^ \circ }$
$ \Rightarrow b = 3x = 3({18^ \circ }) = {54^ \circ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.....\,(7)$
Now, OX is a ray on the line MON.
\[\angle XOM{\text{ }} + \angle XON = {180^ \circ }\]
\[\angle XOM = b,\,\angle XON = c\]
\[b{\text{ }} + {\text{ }}c{\text{ }} = {\text{ }}{180^ \circ }\,\,\,\,\,\,\,\,\,\,.....(8)\] (by Linear Pair axiom)
Substituting equation (7) in equation (8), we get,
\[\begin{array}{*{20}{l}}
  { \Rightarrow {{54}^ \circ } + c = {{180}^ \circ }} \\
  { \Rightarrow c = {{126}^ \circ }}
\end{array}\]
Therefore, the value of c = \[{126^ \circ }\]
Hence, the correct answer is option (A.) ${126^ \circ }$.

Note: The most common mistake while solving this type of questions, occurs when we calculate angles using axioms of linear pair of angles. Another method to find out the value of $\angle XON$ is by adding \[{90^ \circ }\] to a.