Question

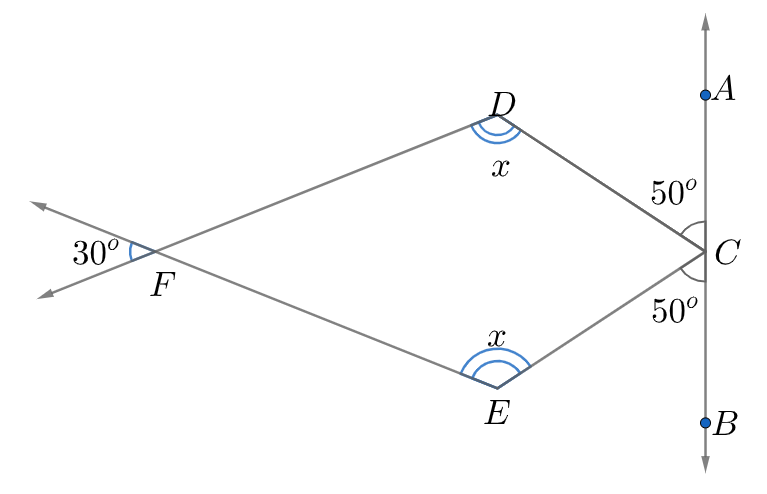
In the given figure, find the angle x:

Answer 1

Hint: For solving these problems, we need to have a clear understanding about the various geometrical figures and the formula regarding their angles. By employing those formulas and using the properties of angles, we can easily find out the value of x in the given figure.

Complete step by step answer:
Geometry is one of the important branches of mathematics that deals with the study of different shapes. It initiates the study of lines and angles. A straight line is a line without curves and it is defined as the shortest distance between two points. An angle is formed when the line segment meets at a point.
First, we need to know that the sum of angles in a polygon with n sides is equal to $\left( n-2 \right)\times {{180}^{\circ }}$ . So, for a quadrilateral with four sides, the sum of angles is equal to $\left( 4-2 \right)\times {{180}^{\circ }}={{360}^{\circ }}$ .
When two lines intersect, the opposite angles are equal hence they are called vertically opposite angles. In the above figure, $\angle DFE$ and ${{30}^{\circ }}$ are vertically opposite angles because the lines intersect at F. Hence, $\angle DFE={{30}^{\circ }}$ .
Two angles are called complementary if their measures add to ${{90}^{\circ }}$ , and called supplementary if their measures add to ${{180}^{\circ }}$ . Now, on a straight line, the sum of angles is ${{180}^{\circ }}$ on each side of the straight line. In the given figure, we can thus say that the sum of angles on the left side of the line ACB is ${{180}^{\circ }}$ . Thus,
$\begin{align}
  & \Rightarrow \angle ACD+\angle DCE+\angle ECB={{180}^{\circ }} \\
 & \Rightarrow {{50}^{\circ }}+\angle DCE+{{50}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow \angle DCE={{80}^{\circ }} \\
\end{align}$
Thus, in the quadrilateral DFEC, $\angle DFE={{30}^{\circ }}$ , $\angle DCE={{80}^{\circ }}$ , $\angle FDC$ and $\angle FEC$ are equal to ${{x}^{\circ }}$ . Now we already know that the sum of angles of a quadrilateral is ${{360}^{\circ }}$ . Hence, we can say that
\[\begin{align}
  & \Rightarrow \angle DFE+\angle DCE+\angle FDC+\angle FEC={{360}^{\circ }} \\
 & \Rightarrow {{30}^{\circ }}+{{80}^{\circ }}+{{x}^{\circ }}+{{x}^{\circ }}={{360}^{\circ }} \\
 & \Rightarrow {{x}^{\circ }}={{125}^{\circ }} \\
\end{align}\]
Thus, using the properties of angles we have arrived at the answer that the value of x in the above figure is \[{{125}^{\circ }}\] .

Note: These types of problems are pretty easy to solve, but one needs to be careful otherwise small misjudgements can lead to a totally different answer. We need to carefully observe the figure employing the correct formula of supplementary and vertically opposite angles. Miscalculations should also be avoided while solving the equations.