Question

In the given figure, equivalent resistance between points P and Q is

(A) $\dfrac{1}{3}\;{\rm{\Omega }}$
(B) $\dfrac{4}{3}\;{\rm{\Omega }}$
(C)$\dfrac{2}{3}\;{\rm{\Omega }}$
(D) $2\;{\rm{\Omega }}$

Answer 1

Hint: In this type of questions, you need to apply the concept of equivalent resistance. Firstly, you need to figure out whether the upper part of the circuit will have an impact on the equivalent resistance or not. This can be done by applying KCL about the junction point. Later you can calculate the equivalent resistance by applying series and parallel combination.

Complete step by step answer:
Let us consider a point, say R at the junction. If we say that the current starts to flow from end P to other branches of the resistors. We can see the flow of the current in the figure given below,

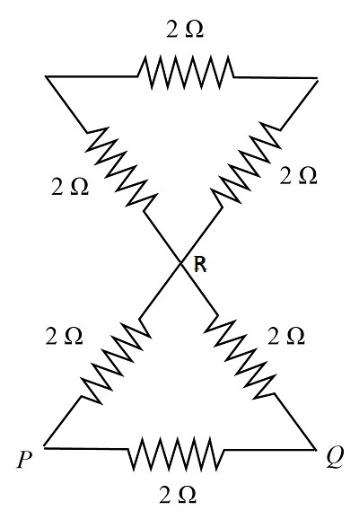
The point R acts as the junction point. So, applying Kirchhoff’s Current Law (KCL) in the circuit, we get,
$I + {I_2} = {I_2} + {I_1}$

Further solving the above expression, we will get,
$I = {I_1}$

From this, we can say that the current will flow the same from point P to R, and then R to Q. The current will not flow through the upper part of the circuit. The remaining circuit we will obtain is,

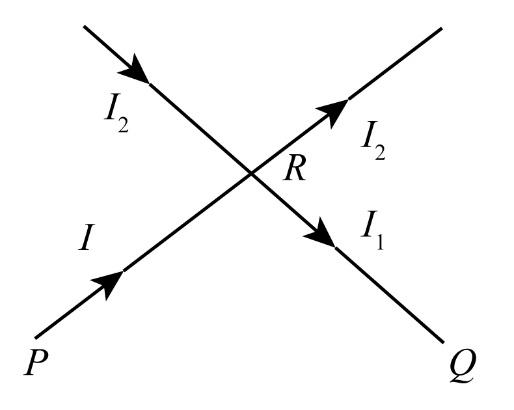
Here, resistors ${R_1}$ and ${R_2}$ are in series combination to each other.

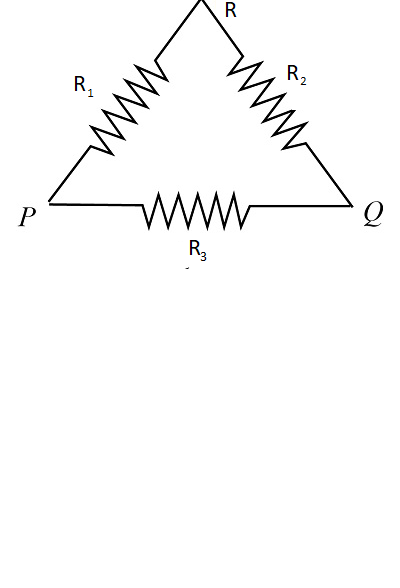
So the equivalent resistor of these both can be calculated as,
$R = {R_1} + {R_2}\\$
$\implies R = {\kern 1pt} 2\;{\rm{\Omega }} + 2\;{\rm{\Omega }}\\$
$\implies R = 4\;{\rm{\Omega }}$

This obtained equivalent resistance is in parallel combination with the resistor ${R_3}$. Therefore, the equivalent resistance of the circuit is given as,
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{R} + \dfrac{1}{{{R_3}}}\\$
$\implies \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{2\;{\rm{\Omega }}}} + \dfrac{1}{{4\;{\rm{\Omega }}}}\\$
$\implies \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{2\;{\rm{\Omega }}}} + \dfrac{1}{{4\;{\rm{\Omega }}}}\\$
$\implies {R_{eq}} = \dfrac{4}{3}\;{\rm{\Omega }}$

Therefore, the equivalent between the point P and Q is $\dfrac{4}{3}\;{\rm{\Omega }}$.

Therefore, the option (B) is the correct answer.

Note:
You can make a mistake in the calculation while considering the upper part for the solution. Although you can use it, it would be lengthy and time-consuming. All the resistance, other than one between point P and Q will be in series. The equivalent resistance obtained will be in parallel combination with the resistor between point P and Q.