Question

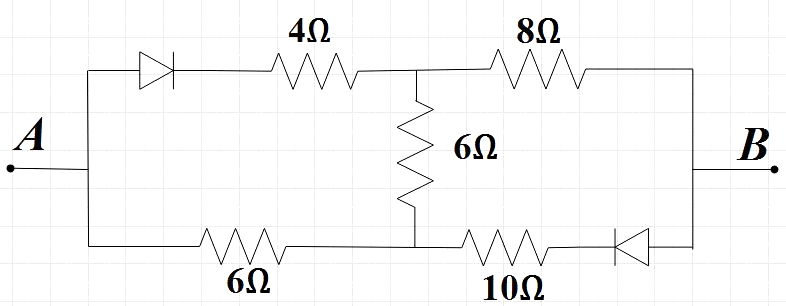
In the given circuit, the equivalent resistance between A and B is (if A has positive potential and B has negative potential)

A. $11\Omega $
B.$\dfrac{34}{3}\Omega $
C. $10\Omega $
D. $8\Omega $

Answer 1

Hint: As a first step, look for the presence of an open circuit in some loop within the circuit, also, remember that when the diode is reverse biased, no current passes through the resistor next to it. Now you could slowly find the equivalent resistance in a step by step manner. Apply the expression for equivalent resistance for series and parallel combination accordingly.
Formula used:
Expression for equivalent resistance:
In parallel,
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$
In series,
${{R}_{eq}}={{R}_{1}}+{{R}_{2}}$

Complete answer:
In the question, we are given a circuit with a combination of some resistors and two diodes. We are asked to find the equivalent resistance across the terminals A and B, if the terminal A was positive and terminal B was negative.

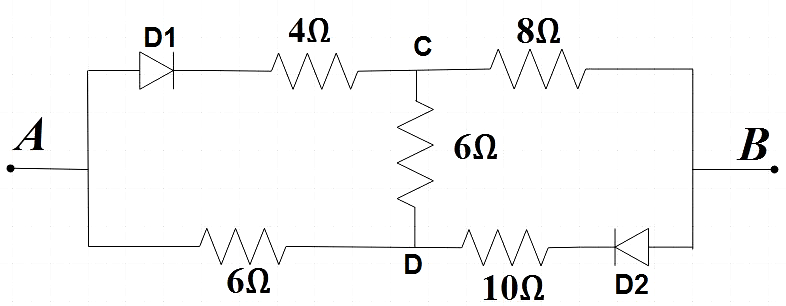
Since the terminal A is positive and B is negative, the diode D2 is reverse biased, and hence we could say that no current passes through the resistor next to it. Hence the connection DB acts as an open circuit. Therefore we could redraw the circuit as,

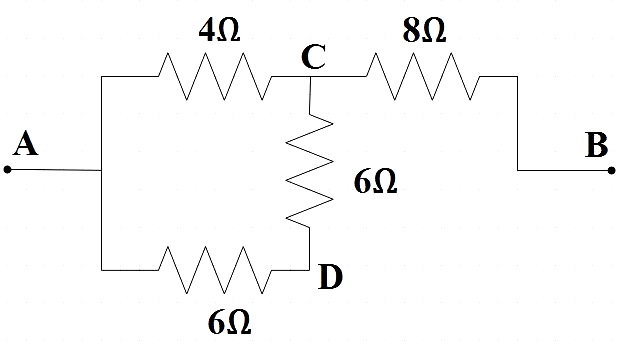
We see that the resistors across AD and DC are in series and we know that the equivalent resistance of a series combination of resistors ${{R}_{1}}$ and ${{R}_{2}}$ are given by,
${{R}_{eq}}={{R}_{1}}+{{R}_{2}}$
Therefore, $\Rightarrow {{R}_{eq}}=6+6=12\Omega $
Now the circuit can be reduced as,

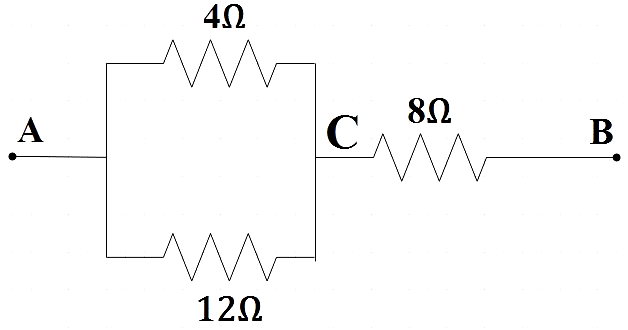
Now we have two resistors connected in parallel across A and C. We know that the equivalent resistance for the parallel connection for resistors ${{R}_{1}}$ and ${{R}_{2}}$ are given by,
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$
$\Rightarrow {{R}_{eq}}=\dfrac{{{R}_{1}}\times {{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$
So equivalent resistance across AC is given by,
${{R}_{eq}}=\dfrac{4\times 12}{4+12}=3\Omega $
Now the given circuit can be further reduced as,

Now we are left with a simple series combination of 2 resistors of resistance $3\Omega $ and $8\Omega $ respectively. Now the equivalent resistance can be given by,
${{R}_{EQ}}=3\Omega +8\Omega $
$\Rightarrow {{R}_{EQ}}=11\Omega $
Therefore, the equivalent resistance between A and B in the given circuit is $11\Omega $

So, the correct answer is “Option A”.

Note:
For questions that involve a number of resistors and diodes, try to simplify the given circuit to the maximum. Also, look for the presence of an open circuit within the given circuit. When diodes are given, make note of which among the given terminals is positive and negative and then work accordingly.